Este tutorial presenta los elementos básicos introductorios al software Vensim para la creación de Diagramas de Ciclos Causales. Se presentan los diferentes ambientes de trabajo que tiene el software, los elementos para construir modelos y un caso sencillo para practicar en la construcción de dichos modelos.

¿Qué aprenderá?

Elementos básicos del software Vensim para la construcción de Diagramas de Ciclos Causales de Dinámica de Sistemas.

¿Qué necesita?

Descargar e instalar la versión "PLE" (Personal Learning Edition) del software Vensim. Las instrucciones detalladas se encuentran en la pestaña "Vensim" de este tutorial.

Descarga e instalación

Vensim es uno de los paquetes de software de simulación disponibles para la construcción de modelos de Dinámica de Sistemas. La apariencia de controles, botones y ventanas que aparecen en este tutorial puede variar según la versión de Vensim que se utilice. Este tutorial se basa en la versión "PLE" que es la versión básica para aprender a construir y simular modelos de Dinámica de Sistemas, no tiene costo para uso educativo.

En el siguiente recurso que aparece en el curso "Descarga Vensim" encontrará los archivos para la descarga e instalación del Software según el sistema operativo que usted utilice.

Imagen 1. Ubicación de archivos de descarga de Vensim.

Asegúrese de instalar la versión PLE que no requiere de licencia.

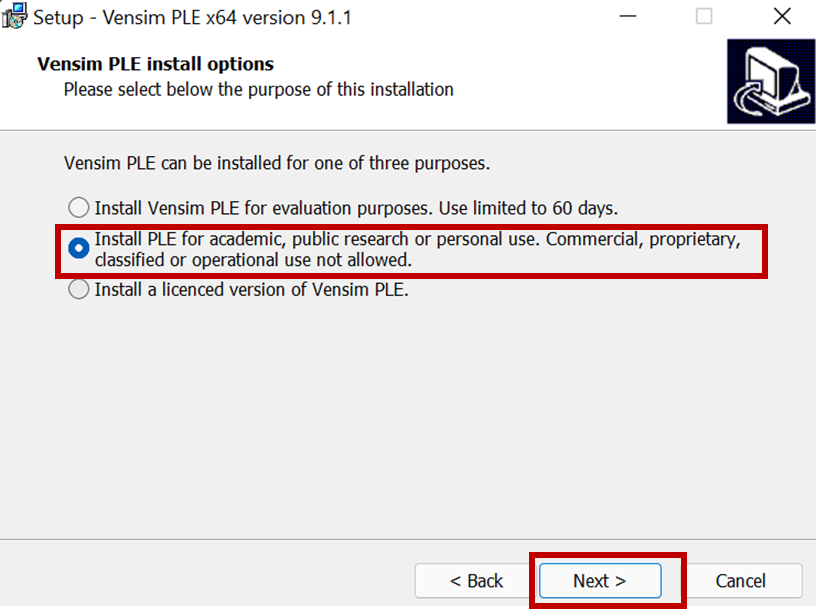
Imagen 2. Instalación versión de uso académico de Vensim.

Por defecto la versión que se descarga utiliza una interfaz en versión beta. Para asegurarnos de que todos utilicemos la misma versión, vamos a cambiar a la visualización anterior haciendo click en "Tools" y después en "Switch Back to Old Sketch". Si no se realiza este cambio, la interfaz que mostramos en el tutorial, posiblemente no coincida con la que vea en su computador.

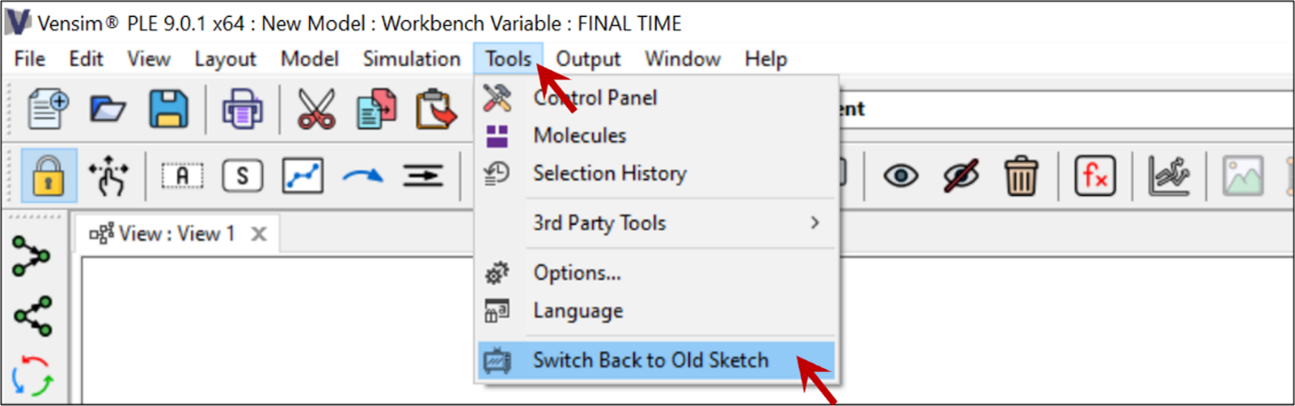
Imagen 3. Cambio la visualización anterior.

Vensim es un software de simulación continua que permite construir y simular modelos de Dinámica de Sistemas. Provee un ambiente de modelado y un lenguaje de alto nivel (es decir, que es adecuado para la capacidad cognitiva humana, opuesto a los lenguajes "de máquina") para construir modelos en un espacio de trabajo con controles y facilidades gráficas que facilitan la representación y simulación computacional. En términos matemáticos, un modelo de Dinámica de Sistemas es un sistema no lineal de ecuaciones diferenciales ordinarias; el software se encarga de formalizar el modelo en ecuaciones de diferencia que resuelve con algoritmos de métodos numéricos.

Vensim trabaja con dos distinciones básicas que maneja por separado: 1) los modelos y, 2) los datos que arrojan los resultados de las simulaciones de los mismos. Los primeros conforman una "estructura" con ecuaciones y variables que se relacionan entre sí, los segundos corresponden a los valores que toman las variables del modelo a lo largo de un horizonte de tiempo cuando se resuelven las ecuaciones, es decir, un "comportamiento". Un pilar de la Dinámica de Sistemas es la comprensión del vínculo entre estructura y comportamiento o, dicho de otra manera, comprender por qué un modelo arroja los resultados de simulación que produce de acuerdo con la forma como variables y ecuaciones están definidas y relacionadas en el modelo.

Cada vez que vamos a crear un nuevo modelo se abre un cuadro de diálogo nuevo para realizar algunos ajustes de configuración antes de comenzar a trabajar; tiene varias pestañas (Time Bounds, Info/Pswd, Sketch, Units Equiv, XLS Files, Ref Modes). Por ahora nos interesa la primera pestaña que se abre por defecto, Time Bounds; esta pestaña nos permite configurar los siguientes elementos:

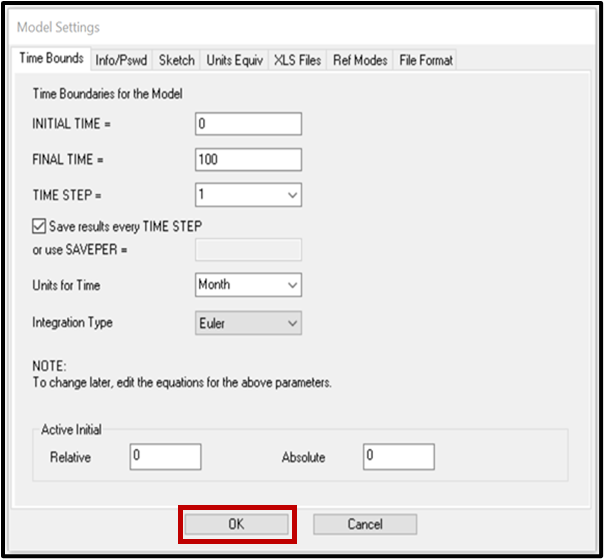
Imagen 4. Configuración del modelo.

• INITIAL TIME: tiempo en el que comienza la simulación.
• FINAL TIME: tiempo en el que termina la simulación.
• TIME STEP: tiempo de intervalo de simulación (DT). Se debe escoger el valor más bajo que prevenga errores de integración; típicamente se utilizan valores entre 0.25 y 1.
• Save results every TIME STEP: si esta opción está seleccionada configura SAVEPER igual a TIME STEP, que es el valor por defecto y aceptable. SAVEPER es la frecuencia a la cual se guardan los resultados de simulación.
• Units for Time: unidades de tiempo de simulación; sirve de referente para todas las variables del modelo.
• Integration Type: define el método de integración que utilizará Vensim para resolver las ecuaciones; por defecto utilizamos el método de Euler y usualmente este será suficiente. Está disponible también el método Runge-Kutta de orden 4 que es más preciso, pero utiliza más recursos computacionales.

Dado que por el momento no se realizarán simulaciones podemos trabajar con los valores por defecto de las especificaciones así que hagamos click en "Ok".

Vensim cuenta con un espacio de trabajo (área en blanco) en el centro de la pantalla, opciones de menú, configuración de simulaciones y controles en la parte superior y varias herramientas de análisis en la parte izquierda; al crear un nuevo modelo o abrir uno ya existente aparecen herramientas de modelado en la parte superior:

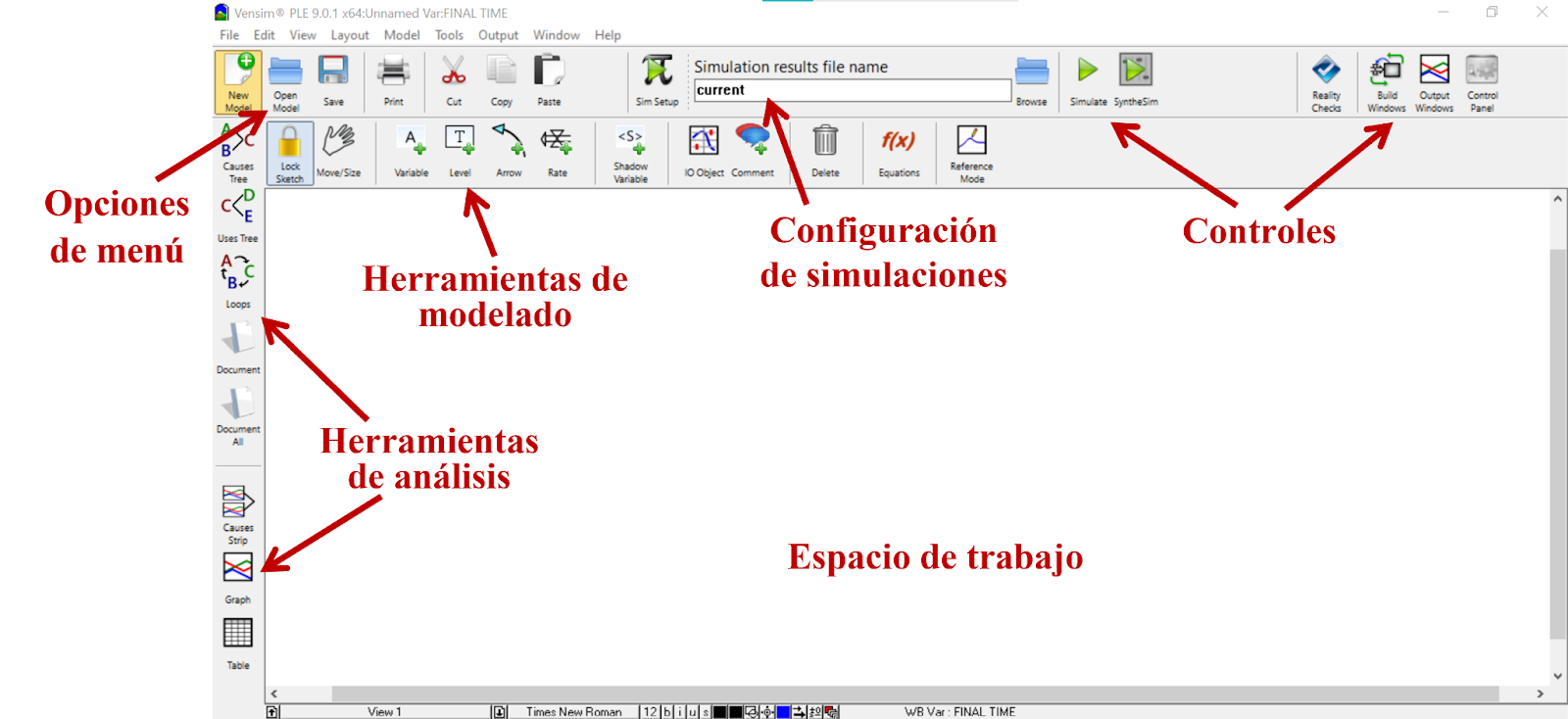
Imagen 5. Herramientas y controles de Vensim.

Los Diagramas de Ciclos Causales (DCC) son medios para representar la estructura de un sistema. En particular son útiles para:

• Capturar rápidamente las hipótesis sobre las causas de las dinámicas. Fundamentalmente nuestras hipótesis estarán fundamentadas en ciclos de realimentación los cuales serán el soporte para la explicación acerca del comportamiento de las variables de interés, en particular de aquellas asociadas a la situación problemática que estemos tratando.
• Representar los modelos mentales de personas y equipos de trabajo, es decir, las teorías, creencias e hipótesis que tienen diversos actores sobre una situación particular.
• Comunicar y discutir el papel de los procesos de realimentación en relación con los problemas que enfrentamos.
• Conceptualizar situaciones problemáticas. Esta conceptualización puede servir de plataforma para luego construir un modelo de simulación.

En la Imagen 6 se observa un DCC compuesto de 3 variables genéricas (Variable X, Variable Y y Variable Z) que interactúan entre sí por medio de los enlaces que las conectan.

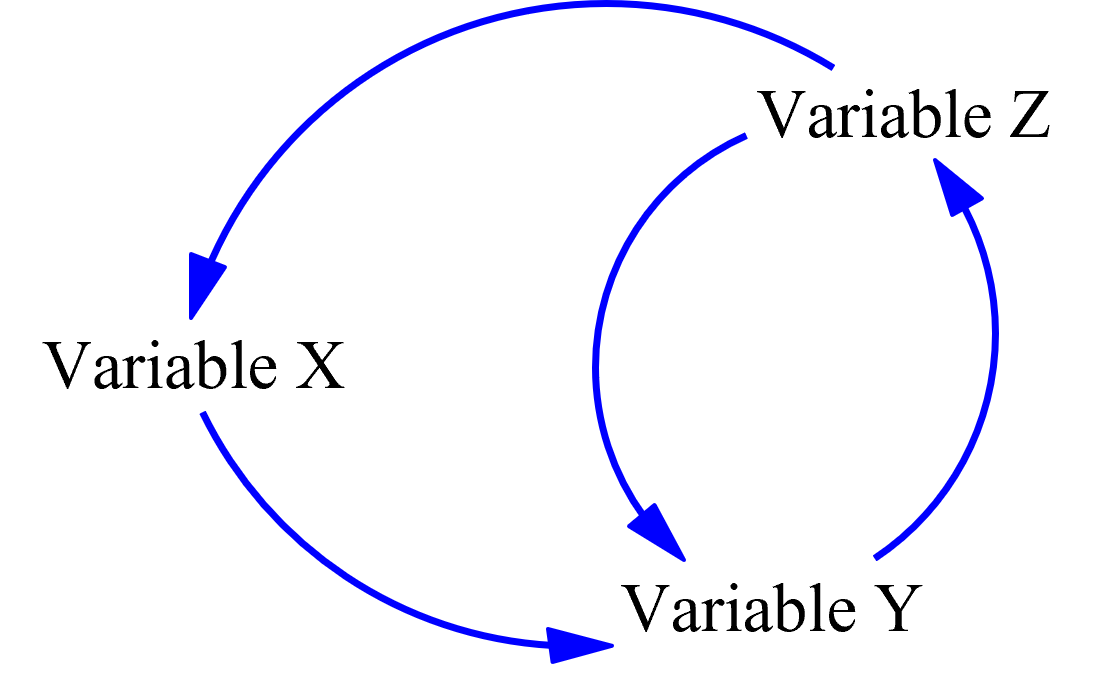
Imagen 6. Ejemplo de un DCC con variables genéricas.

Elementos para construir un Diagrama de Ciclos Causales en Vensim

Un Diagrama de Ciclos Causales consta de dos elementos:

Imagen 7. Elementos para la construcción de DCC.

Variable: son dependientes o independientes que representan la toma de decisión de los actores. Ejemplos: valor del salario mínimo, número de empleados a contratar, precio de venta de un artículo, unidades a producir, etc. Se representan mediante el nombre con el que se quiere denominar a la variable; por ejemplo, en la Imagen 6 la variable se llama "X".

Enlace causal: los enlaces causales establecen una relación de causalidad entre dos variables. La dirección del enlace indica la dirección en la que se produce el efecto de una variable sobre otra. Por ejemplo, x 🡪 y, indica que cuando la Variable X cambia también cambia la Variable Y.

Un Diagrama de Ciclos Causales está compuesto por variables las cuales están conectadas por enlaces causales (flechas); estas relaciones denotan influencias causales entre dichas variables. Por ejemplo:

Ej. 1 – La cantidad de nacimientos tiene un efecto sobre la cantidad de personas en una población

Imagen 8. Ejemplo de relación de causalidad entre los nacimientos y la población.

Ej. 2 – La calidad de trabajo tiene un efecto sobre la efectividad de los resultados

Imagen 9. Ejemplo de relación de causalidad entre la calidad del trabajo y la efectividad de resultados.

Ej. 3 – La productividad tiene un efecto sobre las tareas acumuladas

Imagen 10. Ejemplo de relación de causalidad entre la productividad y las tareas acumuladas.

A continuación, veremos cómo construir estos modelos en Vensim.

1. Variables

• En la sección de Herramientas de modelado, seleccionar el ícono de variable ("Variable", un click):

Imagen 11. Insertar una variable.

• Mover el cursor al sitio en donde se va a poner la variable en el espacio de trabajo y depositarlo con un click.
• Escribir el nombre de la variable e.g. "Nacimientos" y oprimir <Enter>.
• Escribir el nombre de la variable e.g. "Población" y oprimir <Enter>.

Imagen 12. Variables "Nacimientos" y "Población".

Sugerencia: los nombres de las variables deben ser sustantivos (nombres) o frases "sustantivas". Las acciones (verbos) son capturadas por los enlaces que conectan las variables. Por ejemplo, si se tiene un aumento en los nacimientos que genera un aumento en la población, como se ve en la Imagen 13, sería correcto llamar la variable "Nacimientos" y la otra variable "Población" y el enlace que conecta las variables captura el comportamiento de una variable a otra. Por eso mismo, sería incorrecto llamar la variable "Aumento de nacimientos" y "Aumento de población".

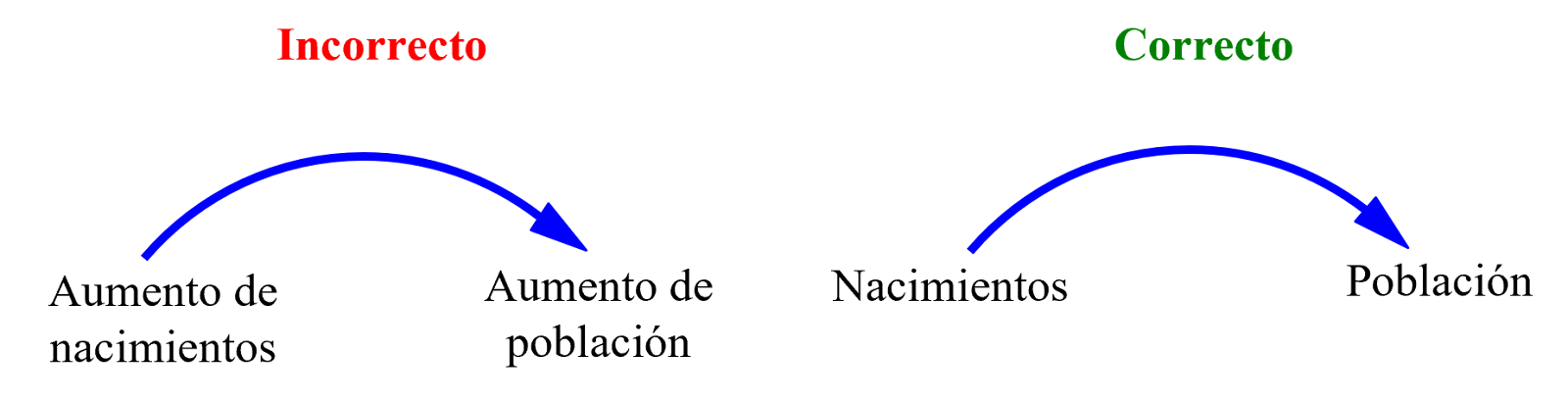
Imagen 13. Nombrar variables en un modelo.

2. Enlaces

Es necesario crear primero las variables para luego conectarlas con los enlaces causales. Para crear los enlaces

• Seleccionar (haciendo click) la opción de "Arrow" en las Herramientas de modelado:

Imagen 14. Crear un enlace causal.

• Hacer click en la variable "Nacimientos" y luego hacer click en la variable "Población". Esto creará un enlace desde la variable "Nacimientos" a la variable "Población".

Imagen 15. Enlace causal entre "Nacimientos" y "Población".

En la Imagen 15 se puede evidenciar que el enlace generado es una línea recta entre las dos variables. Cuando se genera un DCC tener todos los enlaces rectos puede generar confusiones en la visualización de las variables y sus relaciones causales, por esto, es recomendable arreglar la curvatura de las flechas para darle la forma deseada.

• El enlace se hace curvo seleccionando el círculo pequeño en la mitad de la flecha y moviéndolo para generar la curva de interés.

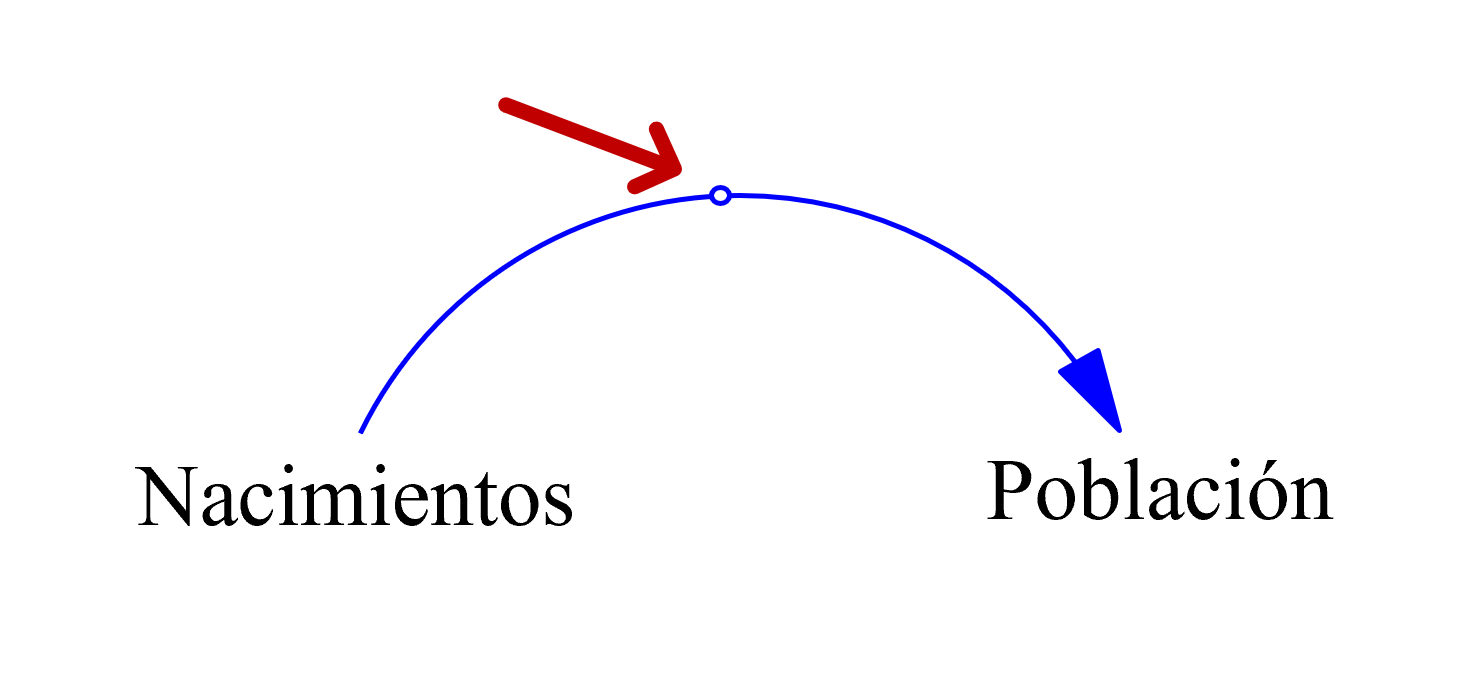
Imagen 16. Hacer enlace curvo.

La Imagen 17 evidencia el resultado final del enlace causal curvo entre las variables "Nacimientos" y "Población".

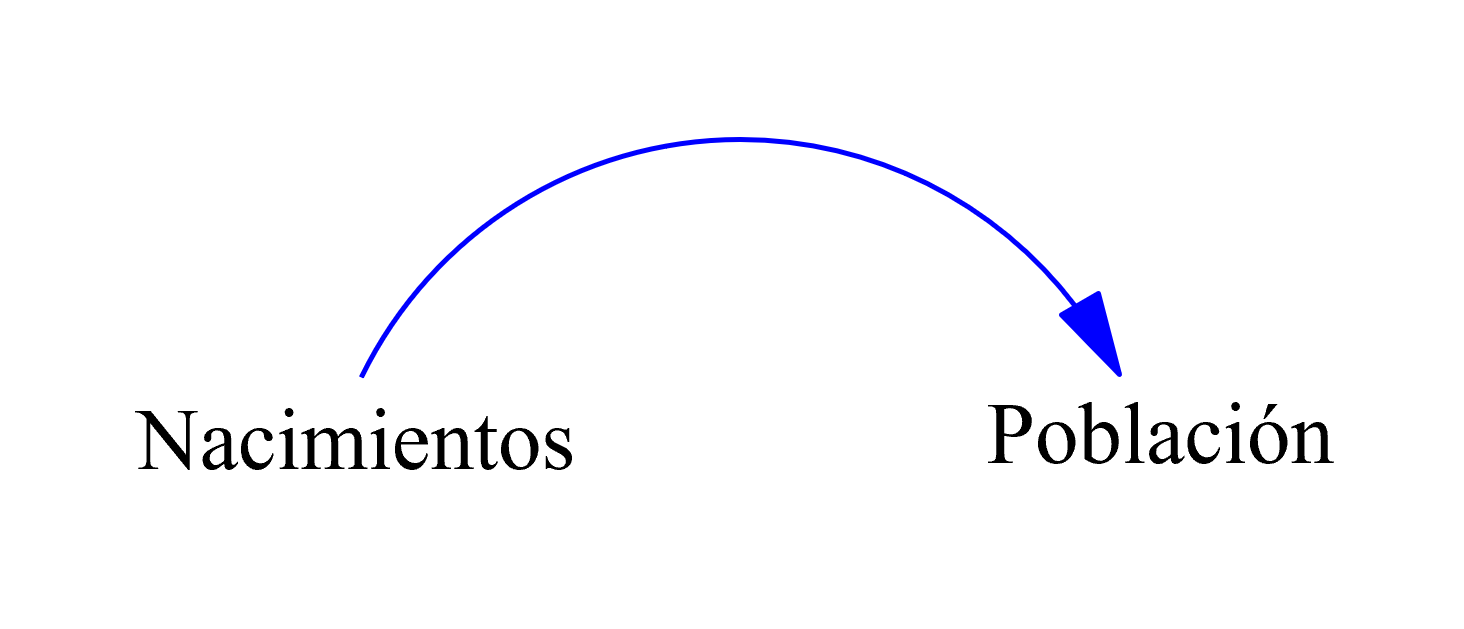
Imagen 17. Enlace causal curvo entre "Nacimientos" y "Población".

Para modificar las opciones del enlace se puede hacer click derecho en la cabeza o en el círculo pequeño en la mitad de la flecha (como se ve en la Imagen 16) para desplegar el siguiente menú:

Imagen 18. Configuración de enlaces causales.

La opciones modificables en un enlace son (Imagen 18):

1. Representar demoras entre variables seleccionando la caja de "Delay mark".
2. Modificar el color del enlace.
3. Cambiar el estilo de línea del enlace, así como su grosor.
4. Determinar la polaridad del enlace. Se puede utilizar la convención tradicional de "+" para polaridades positivas y "-" para polaridades negativas; la letra "S" corresponde también a una polaridad positiva (por su traducción en inglés de "same" que indica que cambian en la misma dirección) o la letra "O" corresponde a una polaridad negativa (por su traducción al inglés de "opposite" que indica que cambian en direcciones opuestas). Se recomienda utilizar los signos "+" y "-" cuyo uso es más frecuente.
5. Seleccionar la posición en la que se desea mostrar la polaridad en la flecha.

A lo largo del tutorial encontrará cómo y cuándo utilizar cada una de las configuraciones de los enlaces causales mostradas en la Imagen 18.

3. Polaridades de enlaces causales

Los enlaces causales pueden ser de diferente tipo dependiendo del efecto que tiene una variable sobre otra. Podríamos decir que cuando el cambio en una variable produce un cambio en la misma dirección en otra variable (es decir, un aumento en una produce un aumento en la otra, o una disminución en una produce una disminución en la otra) significa que la relación entre ese par de variables tiene una polaridad positiva y la indicaremos con un signo "+" o con la letra "S" (por su traducción en inglés: "Same direction").

Si por el contrario el cambio en una variable produce un cambio en la dirección opuesta en otra variable (es decir, un aumento en una variable produce una disminución en otra, o una disminución en una variable produce un aumento en otra) significa que la relación tiene una polaridad negativa y la indicaremos con un signo "-" o con la letra "O" (por su traducción en inglés: "Opposite direction") sobre la flecha que las relaciona.

En el ejemplo de nacimientos y población, mostrado anteriormente, podríamos preguntarnos ¿En qué dirección van los cambios asociados a las situaciones anteriores? Por ejemplo:

• ¿Cómo cambiaría el nivel de población si hubiera más nacimientos? ¿Cuál sería la polaridad entre los nacimientos y la población?
• ¿Un aumento en la calidad del trabajo aumenta o disminuye la efectividad? ¿Cuál sería la polaridad entre la calidad del trabajo y la efectividad?
• ¿Cómo cambiarían las tareas acumuladas si la productividad aumenta? ¿Y si disminuye? ¿Cuál sería la polaridad entre la productividad y las tareas acumuladas?

Para expresar estas polaridades con la herramienta de Vensim, se utiliza el menú de la flecha visto en la sección Enlaces. Al seleccionar la flecha se despliega el menú:

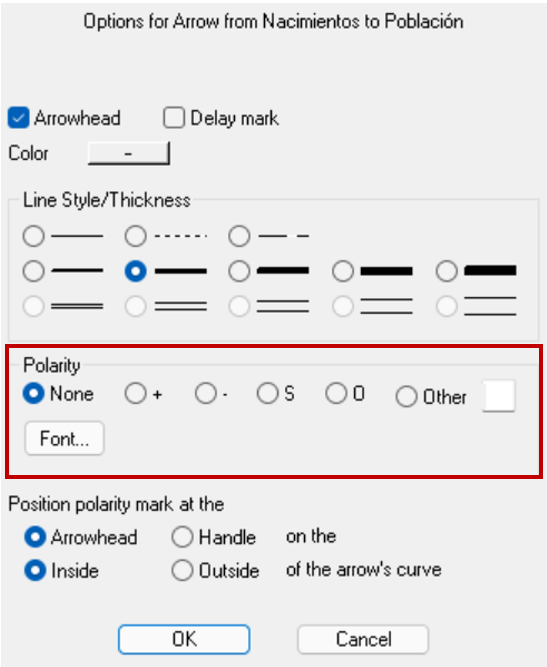
Imagen 19. Selección de polaridad.

En la sección del menú "Polarity", resaltado en la Imagen 18, se debe seleccionar la opción que representa la polaridad entre las dos variables de interés, de acuerdo con las posibles relaciones que se presentaron previamente. Además, con la opción de "Font" se despliegan las siguientes opciones para cambiar el estilo, color y tamaño de la polaridad.

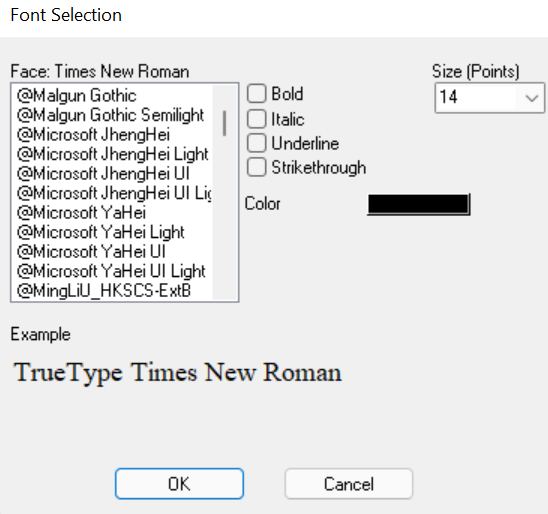
Imagen 20. Configuración de estilo de la polaridad.

También podemos cambiar la ubicación de la polaridad seleccionada, escogiendo la ubicación deseada en la sección del menú "Position polarity mark at the", que se indica en la Imagen 20.

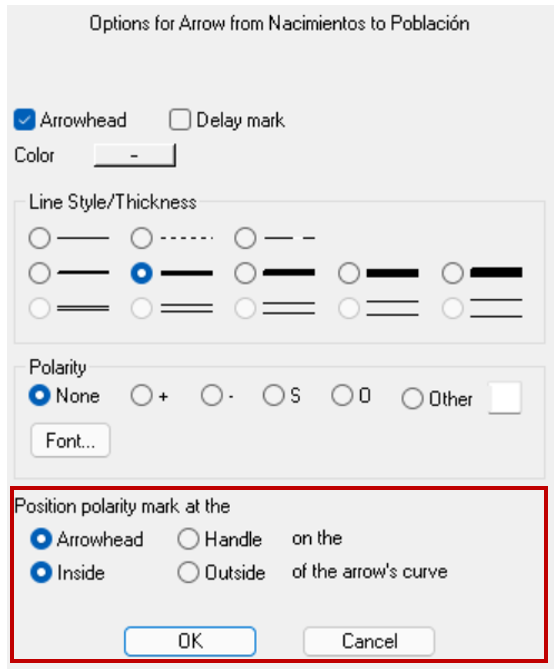
Imagen 21. Configuración de la ubicación de la polaridad.

Como se evidencia en la Imagen 21, se puede seleccionar si se ubica la polaridad en la cabeza de la flecha ("Arrowhead"), en la manija o círculo pequeño en la flecha ("Handle") y, si se desea ubicar la polaridad en la parte interior o exterior de la curvatura de la flecha ("Inside" y "Outside", respectivamente).

En el caso del modelo de población, se podría determinar un enlace positivo de Nacimientos a Población, debido a que un incremento en los Nacimientos conlleva a un incremento en la Población. Para esto:

• Desplegar el menú de la flecha y seleccionar la polaridad positiva "+".
• Hacer click en la opción "+" de la polaridad.
• Seleccionar la opción de "Handle" y "Outside" para ubicar la polaridad en la manija en orientación exterior.
• Dejar las características de Font con las opciones preestablecidas.
• Seleccionar "OK".

El resultado de esta polaridad se muestra en la imagen 22:

Imagen 22. Polaridad de enlace causal entre "Nacimientos" y "Población".

Podemos crear también una nueva variable que se llame "Muertes" e incluirla en el modelo que ya tenemos, establecer el enlace causal correspondiente y su polaridad que en este caso es negativa (si aumentan las muertes disminuye la población).

Imagen 23. Agregar la variable "Muertes" al modelo.

Finalmente, las variables y enlaces del modelo pueden moverse o eliminarse con las Herramientas de Modelado "Move/Size" y "Delete", respectivamente.

Imagen 24. Herramienta para mover y cambiar el tamaño de las variables

Al seleccionar la herramienta y luego el elemento deseado podrá moverlo, ajustar su tamaño o borrarlo.

Los efectos de una acción pueden ser a su vez causa de la misma. Por ejemplo, los resultados de nuestras acciones definen la situación que enfrentaremos en el futuro; la nueva situación afecta nuestra apreciación del problema y las decisiones que tomaremos mañana sobre las mismas variables; además, tenemos que considerar también los efectos de las acciones que tomamos y de las acciones que toman otros agentes cuando reaccionan a nuestras decisiones. Este pensamiento de sistemas resalta el rol que juegan las interacciones y los procesos de realimentación.

Los ciclos de realimentación se clasifican en dos tipos según las dinámicas que pueden generar. Por una parte, un ciclo de realimentación es positivo o de refuerzo si amplifica (o "refuerza") las acciones u operaciones a lo largo de la ruta del ciclo. En cambio, un ciclo de realimentación es negativo o de balance si contrarresta una acción o un estado del mundo como resultado de un actor que busca estabilizar una situación o alcanzar alguna meta.

Pensando el ejemplo de población planteado previamente, podemos caer en la cuenta de que la población debería afectar también los nacimientos (entre más gente haya en la población más gente nacerá) y que la población también afecta las muertes (entre más gente haya en la población más gente morirá). Vamos entonces a modificar el modelo para que los nacimientos y las muertes dependan de la población.

1. Construcción de ciclos

• Crear los enlaces causales de "Población" a "Nacimientos" y de "Población" a "Muertes".
• Definir la polaridad de los nuevos enlaces causales.

El modelo resultante se muestra a continuación:

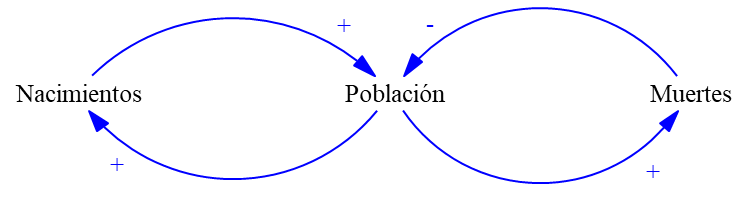
Imagen 25. Enlaces causales de "Población" a "Nacimientos" y "Muertes".

2. Demoras

Nos interesa capturar en nuestros modelos las dinámicas que ocurren a través del tiempo en los sistemas y por esto nos interesa reconocer cuándo el efecto que tiene una variable sobre otra ocurre en un lapso considerable de tiempo; a esto lo llamaremos "demora". Ejemplos de demoras son el tiempo que toma terminar una tarea para así disminuir la cantidad de tareas pendientes, el tiempo de vida de una persona hasta el momento en que muere o el tiempo que toma producir las unidades en una línea de producción.

Para señalar las demoras en los DCC indicaremos si el efecto de una variable sobre otra toma un tiempo a través de dos líneas paralelas en el enlace que conecta a las variables. Podríamos pensar en el tiempo de vida de una persona después del cual muere; esto quiere decir que el efecto de la variable "Población" sobre la variable "Muertes" tiene una demora asociada. Para señalar esta demora en el modelo debemos:

• Hacer click derecho en la cabeza del enlace causal que va de "Población" hacia "Muertes".
• Seleccionar la opción "Delay mark".
• Hacer click en "Ok".

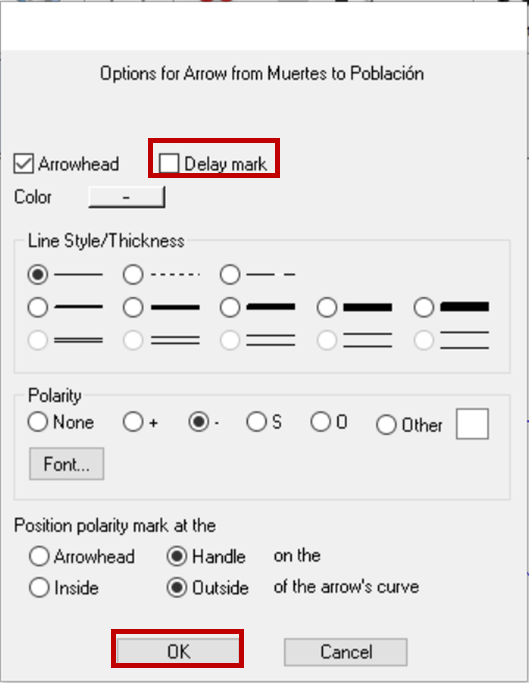
Imagen 26. Definir una demora en un enlace causal.

Una vez definida la demora aparecerá en el enlace causal dos líneas paralelas que indican dicha demora.

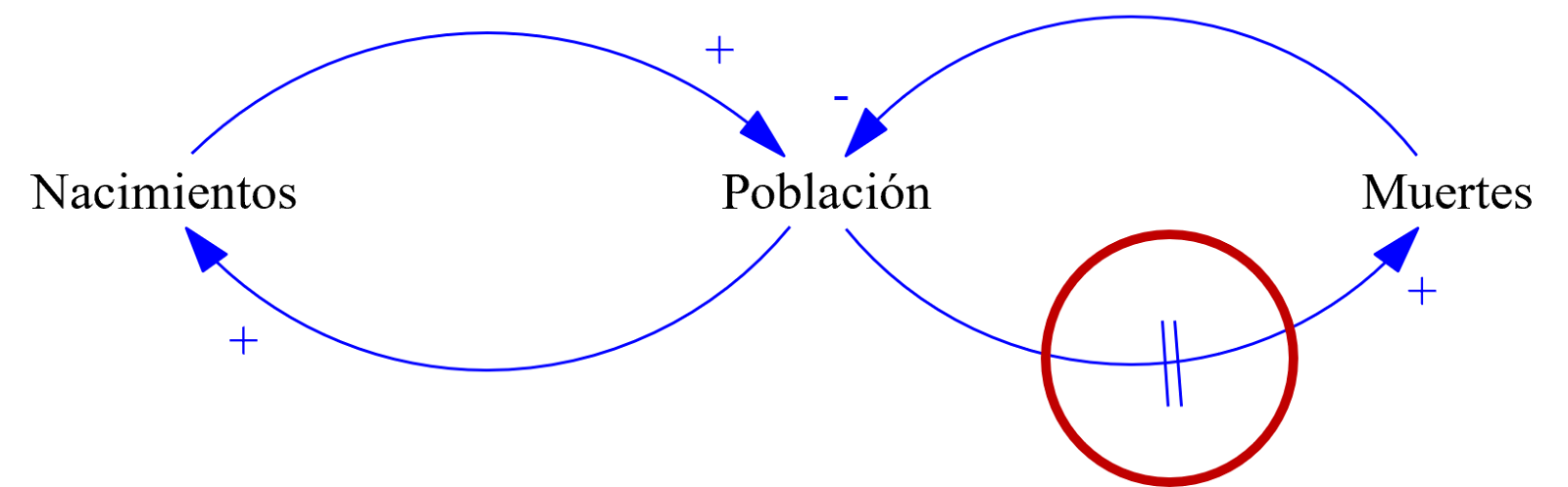
Imagen 27. Demora entre la variable "Población" y la variable "Muertes".

3. Ciclos de Realimentación

Todos los sistemas que modelamos tendrán dos tipos de ciclos de realimentación (positivos o de refuerzo, y negativos o de balance) cuyas interacciones determinan las dinámicas de variables de interés.

• Un ciclo de realimentación es positivo o de refuerzo si amplifica lo que esté sucediendo en el sistema, i.e. las ideas de "círculo vicioso" y "círculo virtuoso". Esto quiere decir que el cambio inicial en una variable seguirá ocurriendo en el mismo sentido después de recorrer todas las variables del ciclo. Por ejemplo, si una variable comienza disminuyendo y después de recorrer el ciclo sigue disminuyendo, entonces será un ciclo de refuerzo (o positivo); esto también aplica en el caso en el que la variable comienza aumentando y después de recorrer el ciclo sigue aumentando.
• Un ciclo de realimentación es negativo o de balance si se opone al cambio, estos ciclos contrarrestan y se oponen a los cambios en un sistema, son mecanismos de autocorrección y autorregulación que buscan la estabilización, por lo general hacia una meta establecida o deseada. Esto quiere decir que el cambio inicial en una variable será contrarrestado después de recorrer todas las variables del ciclo. Por ejemplo, si una variable comienza disminuyendo y después de recorrer el ciclo aumenta, entonces será un ciclo de balance (o negativo); esto también aplica en el caso en el que la variable comienza aumentando y después de recorrer el ciclo disminuye.

En la Imagen 27 presenta dos ciclos de realimentación, identifique la polaridad de estos ciclos (si estos ciclos son de refuerzo o de balance). Una vez determinamos la polaridad de cada ciclo procederemos a indicarlo en nuestro DCC en Vensim. Para indicar la polaridad realizamos los siguientes pasos:

• Seleccionar la herramienta de comentarios "Comment" y hacer click en cualquier lugar del espacio del trabajo donde se quiere ubicar el símbolo de polaridad del ciclo.

Imagen 28. Herramienta para agregar comentarios.

Al hacer esto se desplegará un menú con las siguientes opciones (Imagen 29):

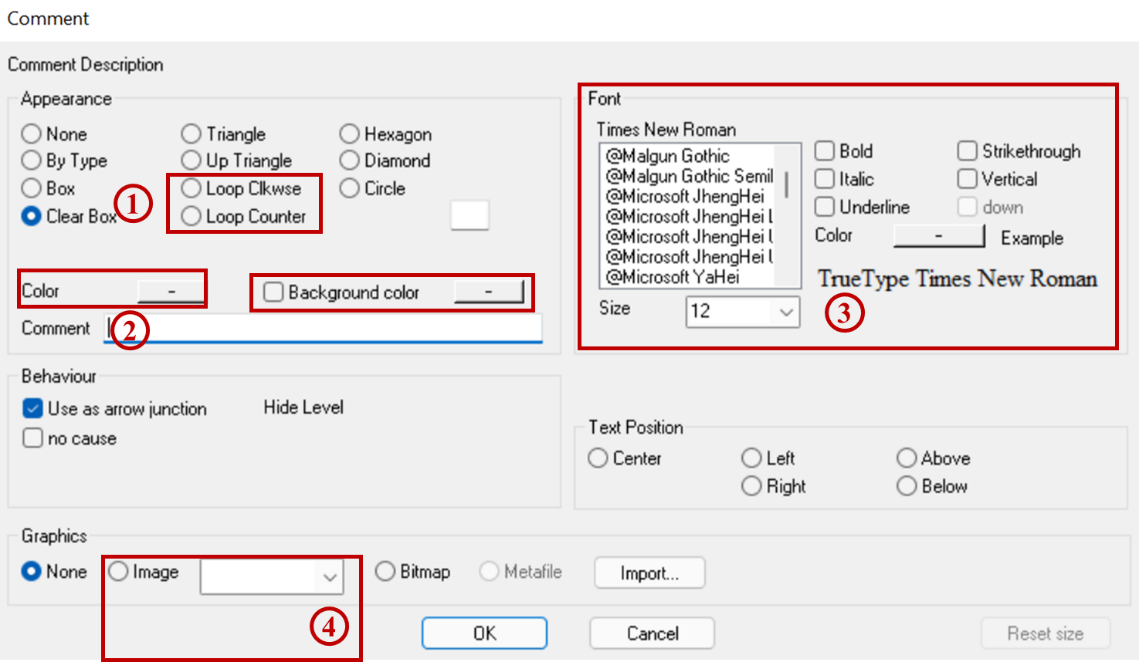
Imagen 29. Menú para configuración de comentarios.

1. Seleccionar figura que rodea el comentario, en este caso utilizaremos "Loop Clokwise" para un símbolo de ciclo teniendo en cuenta el sentido de las manecillas del reloj o "Loop Counter" para un símbolo en el sentido contrario. Acá también se puede seleccionar el color de la figura y el color de fondo de la misma.

• "Loop Clkwise":
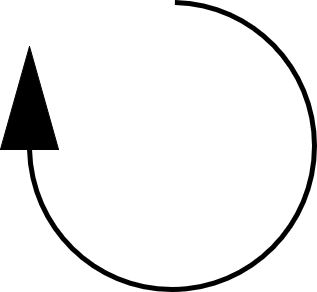
• "Loop Counter":

2. En la barra de comentarios ("Comment") se puede indicar con una "R" o una "B" si el ciclo es de refuerzo o de balance respectivamente.
3. Variaciones al color, tipo y tamaño de letra del comentario.
4. Seleccionando la opción de "Image" se puede también seleccionar el símbolo "+" o "-" para determinar un ciclo de polaridad positiva o negativa respectivamente. Esta es una alternativa para escribir la letra R o B.

Al seguir estos pasos para los ciclos de población determinado se debería obtener el siguiente resultado.

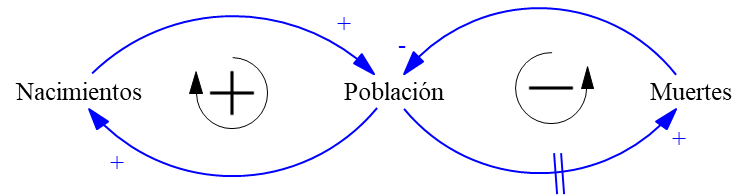
Imagen 30. DCC con polaridades de ciclos.

En modelos más complejos puede haber una gran variedad de ciclos y enlaces causales. Para facilitar la visualización de las rutas de los ciclos de realimentación se pueden utilizar colores o trazos diferentes para los enlaces que los componen. Para hacer esto, seleccione el menú de los enlaces causales (Imagen 31).

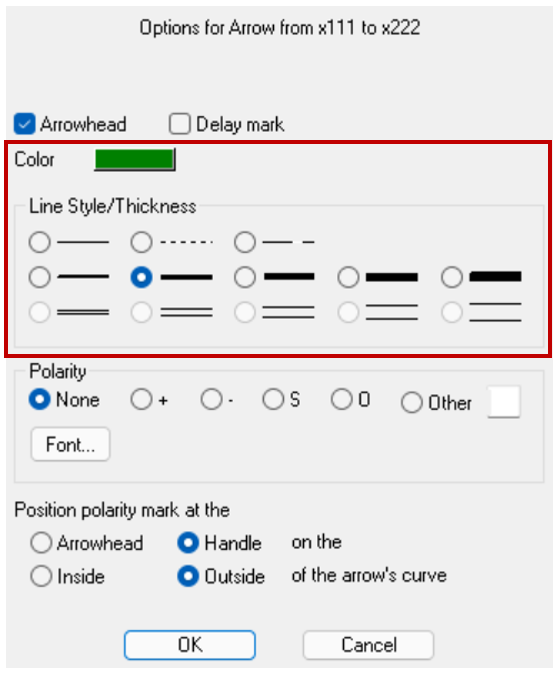
Imagen 31. Configuración color y tipo enlace.

Con la opción de "Color" se podrá escoger entre una variedad de colores que tiene Vensim y con la siguiente sección de "Line Style/Thickness" se podrá escoger entre los tipos de líneas y grosor que se ven en la Imagen 31. Seleccionando el color verde para el ciclo de refuerzo, el color rojo para el ciclo de balance y el grosor indicado en la imagen anterior para todas las flechas del diagrama planteado previamente se obtiene el siguiente resultado:

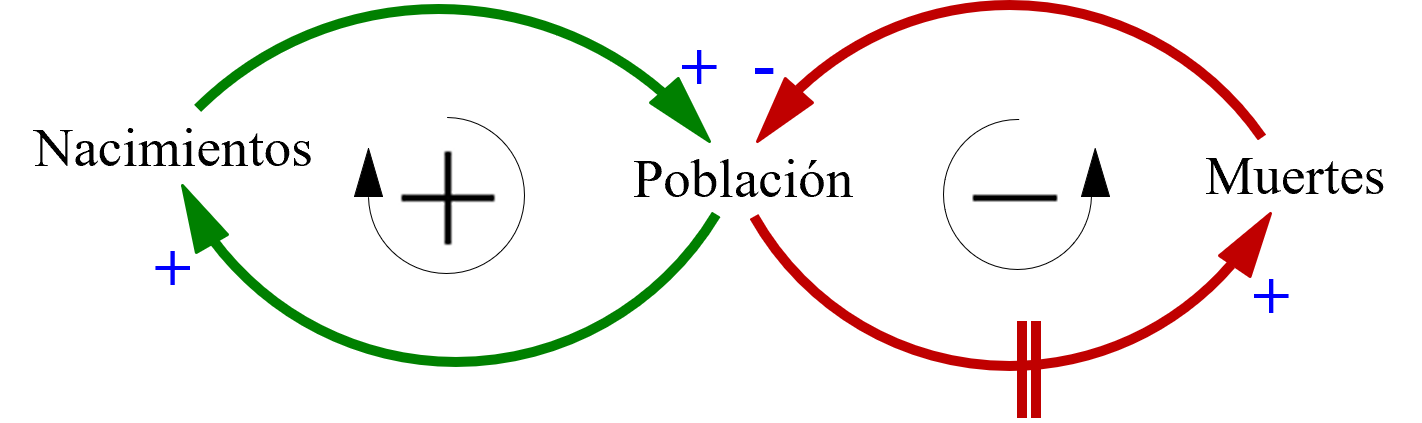
Imagen 32. DCC con color y grosor modificado

En la barra de herramientas de análisis (a la izquierda) varios botones permiten examinar los vínculos causales entre variables. Por ejemplo, ¿cuáles variables afectan a la "Población"? En particular hay que pensar cómo es la relación causal entre Población y la variable Muertes. Conceptualmente es importante notar que son las Muertes las que tienen un efecto negativo en la Población y por lo tanto lo afectan causalmente. Podemos utilizar las herramientas de análisis para construir árboles causales; por ejemplo, para examinar las variables que afectan a la Población hagamos click primero en dicha variable y luego click en el botón "Causes Tree":

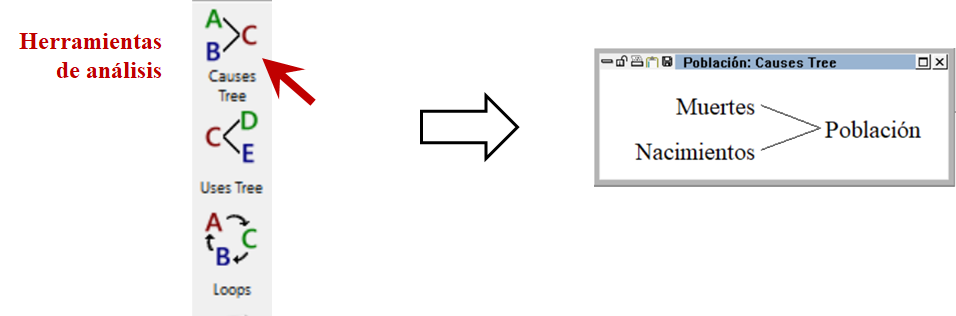
Imagen 33. Herramienta de causalidades.

Se puede cerrar la ventana del árbol causal en la "x" de la esquina superior derecha.

También podemos verificar los ciclos de realimentación que pasan por la variable "Población".

• Hacer click en la variable "Población".
• Hacer click en la herramienta "Loops".

Imagen 34. Herramienta de ciclos.

La ventana de ciclos de realimentación ("Loops") muestra los ciclos que pasan por la variable "Población", en este caso 2 ciclos, cada uno de longitud de 1 (es decir, que están conformados por una variable adicional a "Población").

Versión 1. Mayo 2022