El filtro de Kalman es un algoritmo recursivo que proporciona una estimación óptima del estado de un sistema dinámico a partir de una serie de medidas ruidosas. Es ampliamente utilizado en sistemas de control y navegación, así como en el procesamiento de señales, debido a su capacidad para predecir y corregir estimaciones en tiempo real. Es útil en Sistemas Embebidos debido a su capacidad para procesar datos en tiempo real y su eficiencia computacional. Este filtro es óptimo en el sentido de que minimiza el error cuadrático medio de las estimaciones.

El modelo del sistema se describe mediante dos ecuaciones:

1. Ecuación de Estado (Predictiva):

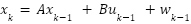
2. Ecuación de Medición (Correctiva):

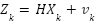
Donde

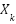es el estado del sistema en el instante .

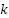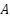es la matriz de transición de estado.

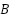es la matriz de control.

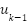es el vector de control en el instante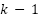

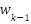es el ruido del proceso (asumido de media cero y covarianza )

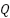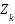es la medición en el instante .

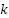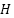es la matriz de observación

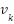es el ruido de medición (asumido de media cero y covarianza )

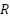Funcionamiento del Filtro de Kalman

El filtro de Kalman realiza dos pasos en cada iteración: predicción y actualización.

1. Predicción:

• Predice el estado siguiente del sistema.
• Predice la covarianza del error.

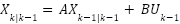
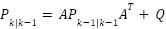
2. Actualización:

• Calcula la ganancia de Kalman.
• Corrige la predicción del estado con la medición.
• Actualiza la covarianza del error.

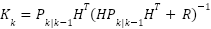
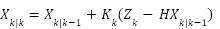
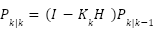
Implementación en ESP32:

Para implementar un filtro de Kalman en una ESP32, se deben definir los estados del sistema, las matrices de transición y de medición, y las matrices de covarianza del proceso y de la medida. A continuación, se muestra un ejemplo simplificado para la estimación de una señal de posición a partir de medidas ruidosas:

struct KalmanFilter {
  float Q; // Variancia del proceso
  float R; // Variancia de la medida
  float A; // Factor de escala del estado (modelo de transición)
  float B; // Control de la entrada
  float C; // Factor de escala de la medida
  float x; // Estimación del estado
  float cov; // Covarianza del estado

  KalmanFilter(float q, float r, float a, float b, float c) 
    : Q(q), R(r), A(a), B(b), C(c), x(0), cov(0) {}

  void predict(float u) {
    x = A * x + B * u;
    cov = A * cov * A + Q;
  }

  void update(float z) {
    float K = cov * C / (C * cov * C + R);
    x = x + K * (z - C * x);
    cov = (1 - K * C) * cov;
  }

  float getState() {
    return x;
  }
};

KalmanFilter kf(0.1, 1.0, 1.0, 0.0, 1.0); // Inicializa el filtro de Kalman con parámetros

void setup() {
  Serial.begin(115200);
}

void loop() {
  float measurement = analogRead(34); // Leer el canal ADC
  kf.predict(0); // No hay entrada de control en este ejemplo
  kf.update(measurement);
  Serial.println(kf.getState());
  delay(100);
}

Explicación del Código.

Estructura del Filtro de Kalman:

• Se define una estructura KalmanFilter que contiene los parámetros y variables necesarias para el filtro de Kalman.
• Los parámetros incluyen las varianzas del proceso (Q) y de la medida (R), los factores de escala del estado (A), del control (B) y de la medida (C), así como la estimación del estado (x) y la covarianza del estado (cov).

Método predict:

• Calcula la predicción del próximo estado del sistema utilizando la ecuación de estado.
• Actualiza la covarianza del estado.

Método update:

• Calcula la ganancia de Kalman.
• Corrige la estimación del estado con la medida.
• Actualiza la covarianza del estado.

Inicialización del Filtro:

• Se crea una instancia del filtro de Kalman con valores iniciales para Q, R, A, B y C.

Bucle Principal:

• En el bucle loop, se lee una medida del ADC.
• Se llama al método predict para predecir el siguiente estado.
• Se llama al método update para actualizar la estimación con la medida.
• Se imprime la estimación del estado.

Aplicaciones.

El filtro de Kalman es ampliamente utilizado en diversas aplicaciones de Sistemas Embebidos, como Sistemas de Navegación Inercial para la fusión de datos de acelerómetros y giroscopios, proporcionando estimaciones precisas de la posición y la orientación. En robótica para el seguimiento de la posición y la velocidad de robots móviles. También se usa en el procesamiento de Señales Biomédicas para la estimación de parámetros fisiológicos a partir de medidas ruidosas.

Código completo Implementación Filtro Kalman en ESP32

A continuación se presenta el código completo para implementar un Filtro Kalman en la ESP32:

#include <driver/adc.h>

// Definiciones de constantes
#define ADC_CHANNEL ADC1_CHANNEL_0 // GPIO36
#define SAMPLE_RATE 1000 // Frecuencia de muestreo en Hz
#define BUFFER_SIZE 1000 // Tamaño del buffer para almacenar muestras

// Estructura del Filtro de Kalman
struct KalmanFilter {
  float Q; // Variancia del proceso
  float R; // Variancia de la medida
  float A; // Factor de escala del estado (modelo de transición)
  float B; // Control de la entrada
  float C; // Factor de escala de la medida
  float x; // Estimación del estado
  float cov; // Covarianza del estado

  // Constructor del Filtro de Kalman
  KalmanFilter(float q, float r, float a, float b, float c) 
    : Q(q), R(r), A(a), B(b), C(c), x(0), cov(1) {} // Inicializamos cov a 1 en lugar de 0 para evitar división por cero

  // Método de predicción
  void predict(float u) {
    x = A * x + B * u;
    cov = A * cov * A + Q;
  }

  // Método de actualización
  void update(float z) {
    float K = cov * C / (C * cov * C + R);
    x = x + K * (z - C * x);
    cov = (1 - K * C) * cov;
  }

  // Método para obtener el estado estimado
  float getState() {
    return x;
  }
};

// Inicializa el filtro de Kalman con parámetros
KalmanFilter kf(0.1, 1.0, 1.0, 0.0, 1.0);

void setup() {
  Serial.begin(115200); // Inicializa la comunicación serial
  adc1_config_width(ADC_WIDTH_BIT_12); // Configura el ADC para un ancho de 12 bits
  adc1_config_channel_atten(ADC_CHANNEL, ADC_ATTEN_DB_0); // Configura la atenuación del canal ADC
}

void loop() {
  float measurement = analogRead(34); // Leer el valor del canal ADC
  kf.predict(0); // Realiza la predicción (sin entrada de control)
  kf.update(measurement); // Actualiza el filtro con la nueva medida
  Serial.println(kf.getState()); // Imprime el estado estimado
  delay(100); // Espera 100 ms antes de tomar la siguiente muestra
}

El filtro complementario es una técnica sencilla pero eficaz para fusionar datos de múltiples sensores, para combinar señales de sensores que tienen diferentes características de ruido y precisión; particularmente útil en Sistemas Embebidos. Se utiliza comúnmente para combinar datos de acelerómetros y giroscopios en aplicaciones de navegación inercial y control de actitud. El filtro complementario aprovecha las características complementarias de diferentes sensores para proporcionar una estimación más precisa y estable.

En el caso de fusión de datos de un acelerómetro y un giroscopio:

• Acelerómetro: Proporciona una medición precisa de la inclinación a largo plazo, pero es sensible a las vibraciones y el ruido a corto plazo.
• Giroscopio: Proporciona una medición precisa del cambio de inclinación a corto plazo, pero sufre de deriva a largo plazo.

El filtro complementario pondera las señales de ambos sensores de tal manera que se aprovechen sus fortalezas y se minimicen sus debilidades.

Implementación en ESP32:

Un filtro complementario simple para combinar datos de un acelerómetro y un giroscopio puede implementarse de la siguiente manera:

#include <Wire.h>
#include <Adafruit_Sensor.h>
#include <Adafruit_MPU6050.h>

// Crear un objeto para el sensor MPU6050
Adafruit_MPU6050 mpu;

// Parámetros del filtro complementario
float angle = 0.0; // Ángulo inicial
float alpha = 0.98; // Factor de ponderación
float dt = 0.01; // Intervalo de tiempo en segundos (10 ms)

void setup() {
  Serial.begin(115200);
  
  // Inicializar el sensor MPU6050
  if (!mpu.begin()) {
    Serial.println("Failed to find MPU6050 chip");
    while (1) {
      delay(10);
    }
  }
  
  // Configurar el rango del acelerómetro y giroscopio
  mpu.setAccelerometerRange(MPU6050_RANGE_2_G);
  mpu.setGyroRange(MPU6050_RANGE_250_DEG);
  mpu.setFilterBandwidth(MPU6050_BAND_21_HZ);
}

void loop() {
  // Leer los valores del sensor
  sensors_event_t a, g, temp;
  mpu.getEvent(&a, &g, &temp);
  
  // Calcular el ángulo del acelerómetro (en grados)
  float accelAngle = atan2(a.acceleration.y, a.acceleration.z) * 180 / PI;
  
  // Calcular el ángulo del giroscopio (integrar la velocidad angular)
  float gyroRate = g.gyro.x; // Velocidad angular en grados por segundo
  angle = alpha * (angle + gyroRate * dt) + (1 - alpha) * accelAngle;
  
  // Imprimir el ángulo estimado
  Serial.print("Angle: ");
  Serial.println(angle);
  
  // Esperar 10 ms antes de la siguiente lectura
  delay(10);
}

Explicación del Código

1. Incluir Librerías y Crear Objeto del Sensor:

#include <Wire.h>
#include <Adafruit_Sensor.h>
#include <Adafruit_MPU6050.h>

Adafruit_MPU6050 mpu;

• Se incluyen las librerías necesarias para utilizar el sensor MPU6050 y se crea un objeto mpu.

2. Parámetros del Filtro Complementario:

float angle = 0.0; // Ángulo inicial
float alpha = 0.98; // Factor de ponderación
float dt = 0.01; // Intervalo de tiempo en segundos (10 ms)

• Se definen los parámetros del filtro complementario, incluyendo el ángulo inicial, el factor de ponderación (alpha), y el intervalo de tiempo (dt).

3. Función setup:

void setup() {
  Serial.begin(115200);
  
  if (!mpu.begin()) {
    Serial.println("Failed to find MPU6050 chip");
    while (1) {
      delay(10);
    }
  }
  
  mpu.setAccelerometerRange(MPU6050_RANGE_2_G);
  mpu.setGyroRange(MPU6050_RANGE_250_DEG);
  mpu.setFilterBandwidth(MPU6050_BAND_21_HZ);
}

• En esta función, se inicializa la comunicación serial y el sensor MPU6050. Se configuran los rangos del acelerómetro y giroscopio y el ancho de banda del filtro.

4. Función loop:

void loop() {
  sensors_event_t a, g, temp;
  mpu.getEvent(&a, &g, &temp);
  
  float accelAngle = atan2(a.acceleration.y, a.acceleration.z) * 180 / PI;
  float gyroRate = g.gyro.x;
  angle = alpha * (angle + gyroRate * dt) + (1 - alpha) * accelAngle;
  
  Serial.print("Angle: ");
  Serial.println(angle);
  
  delay(10);
}

En esta función, se realiza el ciclo principal del programa:

• Se leen los valores del sensor.
• Se calcula el ángulo utilizando los datos del acelerómetro.
• Se calcula el ángulo utilizando los datos del giroscopio e integrando la velocidad angular.
• Se aplica el filtro complementario para combinar ambas estimaciones.
• Se imprime el ángulo estimado.
• Se espera 10 ms antes de la siguiente lectura.

Aplicaciones en Sistemas Embebidos

El filtro complementario es ampliamente utilizado en aplicaciones donde se requiere una estimación precisa de la orientación o el ángulo de inclinación, tales como:

• Sistemas de Navegación Inercial: Para determinar la orientación de vehículos y robots.
• Control de Actitud en Drones: Para mantener la estabilidad y controlar el vuelo de drones.
• Sensores de Movimiento en Dispositivos Portátiles: Para proporcionar datos de orientación en smartphones y otros dispositivos portátiles.

Los métodos suavizadores de señales son técnicas utilizadas para reducir el ruido y las fluctuaciones no deseadas en una señal, haciendo que la señal resultante sea más suave y más fácil de analizar. En sistemas embebidos, donde los recursos computacionales y de memoria son limitados, es crucial utilizar métodos de suavizado eficientes que no sobrecarguen el sistema. A continuación, se explican algunos de los métodos suavizadores más comunes y su implementación en sistemas embebidos como la ESP32.

1. Filtro de Media Móvil

El filtro de media móvil es uno de los métodos de suavizado más simples. Calcula el promedio de un número fijo de puntos de datos adyacentes en la señal. Este promedio se desplaza a lo largo de la señal para suavizar las fluctuaciones.

Implementación en ESP32:

#define WINDOW_SIZE 10
float window[WINDOW_SIZE];
int windowIndex = 0;
float sum = 0;

void setup() {
  Serial.begin(115200);
}

void loop() {
  float newValue = analogRead(34) * (5.0 / 1023.0); // Leer el canal ADC y convertir a voltaje
  sum = sum - window[windowIndex] + newValue;
  window[windowIndex] = newValue;
  windowIndex = (windowIndex + 1) % WINDOW_SIZE;
  float average = sum / WINDOW_SIZE;
  Serial.println(average);
  delay(100); // Esperar 100 ms antes de la siguiente muestra
}

• Ventana de Tamaño Fijo: Se define una ventana de tamaño WINDOW_SIZE para almacenar los últimos valores leídos.
• Suma de Valores: Se mantiene una suma de los valores en la ventana para calcular el promedio.
• Desplazamiento de la Ventana: Cada nuevo valor se añade a la ventana y el más antiguo se elimina, actualizando la suma y calculando el promedio.

2. Filtro de Media Ponderada Exponencial

El filtro de media ponderada exponencial aplica un peso decreciente a los datos históricos. Cada nuevo valor se multiplica por un factor de suavizado, y se combina con la señal suavizada previa.

Implementación en ESP32:

float alpha = 0.1; // Factor de suavizado
float smoothedValue = 0;

void setup() {
  Serial.begin(115200);
}

void loop() {
  float newValue = analogRead(34) * (5.0 / 1023.0); // Leer el canal ADC y convertir a voltaje
  smoothedValue = alpha * newValue + (1 - alpha) * smoothedValue;
  Serial.println(smoothedValue);
  delay(100); // Esperar 100 ms antes de la siguiente muestra
}

• Factor de Suavizado (alpha): Determina el peso de los valores nuevos frente a los anteriores. Un valor de alpha más bajo da más peso a los valores históricos.
• Actualización Recursiva: La señal suavizada se actualiza recursivamente con cada nuevo valor de entrada.

3. Filtro de Savitzky-Golay

El filtro de Savitzky-Golay suaviza la señal ajustando un polinomio de menor grado a un subconjunto de puntos de datos mediante regresión lineal. Es eficaz para mantener las características importantes de la señal, como picos y valles, mientras reduce el ruido.

Implementación en ESP32:

Para implementar un filtro de Savitzky-Golay en una ESP32, se pueden utilizar librerías disponibles o escribir el algoritmo de convolución manualmente. A continuación, se muestra un ejemplo simplificado utilizando una ventana y coeficientes predefinidos.

#define WINDOW_SIZE 5
int coefficients[WINDOW_SIZE] = {-3, 12, 17, 12, -3}; // Coeficientes de Savitzky-Golay
int normalizing_factor = 35; // Suma de los coeficientes
float window[WINDOW_SIZE];
int windowIndex = 0;

void setup() {
  Serial.begin(115200);
}

void loop() {
  float newValue = analogRead(34) * (5.0 / 1023.0); // Leer el canal ADC y convertir a voltaje
  window[windowIndex] = newValue;
  windowIndex = (windowIndex + 1) % WINDOW_SIZE;
  
  float smoothedValue = 0;
  for (int i = 0; i < WINDOW_SIZE; i++) {
    smoothedValue += window[(windowIndex + i) % WINDOW_SIZE] * coefficients[i];
  }
  smoothedValue /= normalizing_factor;

  Serial.println(smoothedValue);
  delay(100); // Esperar 100 ms antes de la siguiente muestra
}

• Coeficientes de Savitzky-Golay: Definen cómo se ponderan los puntos de datos en la ventana para calcular la señal suavizada.
• Normalización: El valor suavizado se normaliza dividiéndolo por la suma de los coeficientes.

Aplicaciones en Sistemas Embebidos

Los métodos suavizadores de señales son fundamentales en diversas aplicaciones de sistemas embebidos, tales como:

• Monitoreo de Sensores: Suavizar datos de sensores para eliminar ruido y mejorar la precisión de las mediciones en aplicaciones industriales, agrícolas o de salud.
• Procesamiento de Señales Biomédicas: Filtrar señales biomédicas como ECG y EEG para obtener datos más claros y útiles para el diagnóstico.
• Control de Sistemas: Reducir las fluctuaciones y el ruido en las señales de retroalimentación de controladores de sistemas embebidos.