La normalización y el escalado son técnicas de preprocesamiento de datos esenciales en el análisis de señales y en el machine learning. Estas técnicas se utilizan para ajustar los rangos de valores de los datos, mejorando la consistencia y facilitando el procesamiento posterior. En sistemas embebidos, donde los recursos computacionales y de memoria son limitados, la implementación eficiente de normalización y escalado es crucial para el rendimiento de los algoritmos. A continuación, se explican en detalle los conceptos, métodos y aplicaciones de la normalización y escalado orientados a sistemas embebidos.

Normalización y Escalado.

La normalización ajusta los valores de una señal para que caigan dentro de un rango específico, típicamente entre 0 y 1, o -1 y 1. Métodos comunes incluyen la normalización Min-Max y la normalización Z-score. El escalado ajusta la amplitud de la señal para que todas las características tengan la misma importancia. Métodos comunes incluyen el escalado lineal y el escalado robusto.

Normalización Min-Max: La normalización Min-Max ajusta los datos para que caigan dentro de un rango especificado [0, 1]. Esto se logra restando el valor mínimo de los datos y dividiendo por el rango (máximo - mínimo).

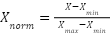
Código de Ejemplo Implementación en ESP32:

#define NUM_SAMPLES 100

float data[NUM_SAMPLES];
float normalizedData[NUM_SAMPLES];
float minValue, maxValue;

void setup() {
  Serial.begin(115200);

  // Simular datos de entrada
  for (int i = 0; i < NUM_SAMPLES; i++) {
    data[i] = analogRead(34); // Leer el valor del ADC
  }

  // Calcular valores mínimo y máximo
  minValue = data[0];
  maxValue = data[0];
  for (int i = 1; i < NUM_SAMPLES; i++) {
    if (data[i] < minValue) minValue = data[i];
    if (data[i] > maxValue) maxValue = data[i];
  }

  // Normalizar los datos
  for (int i = 0; i < NUM_SAMPLES; i++) {
    normalizedData[i] = (data[i] - minValue) / (maxValue - minValue);
  }

  // Imprimir los datos normalizados
  for (int i = 0; i < NUM_SAMPLES; i++) {
    Serial.println(normalizedData[i]);
  }
}

void loop() {
  // No se necesita código en el loop para este ejemplo
}

Normalización Z-score: La normalización Z-score transforma los datos para que tengan una media de 0 y una desviación estándar de 1. Es útil cuando los datos tienen una distribución normal.

donde 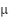es la media y 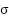es la desviación estándar.

Código de Ejemplo Implementación en ESP32:

#define NUM_SAMPLES 100

float data[NUM_SAMPLES];
float normalizedData[NUM_SAMPLES];
float meanValue, stdDev;

void setup() {
  Serial.begin(115200);

  // Simular datos de entrada
  for (int i = 0; i < NUM_SAMPLES; i++) {
    data[i] = analogRead(34); // Leer el valor del ADC
  }

  // Calcular la media
  meanValue = 0;
  for (int i = 0; i < NUM_SAMPLES; i++) {
    meanValue += data[i];
  }
  meanValue /= NUM_SAMPLES;

  // Calcular la desviación estándar
  stdDev = 0;
  for (int i = 0; i < NUM_SAMPLES; i++) {
    stdDev += (data[i] - meanValue) * (data[i] - meanValue);
  }
  stdDev = sqrt(stdDev / NUM_SAMPLES);

  // Normalizar los datos
  for (int i = 0; i < NUM_SAMPLES; i++) {
    normalizedData[i] = (data[i] - meanValue) / stdDev;
  }

  // Imprimir los datos normalizados
  for (int i = 0; i < NUM_SAMPLES; i++) {
    Serial.println(normalizedData[i]);
  }
}

void loop() {
  // No se necesita código en el loop para este ejemplo
}

Escalado Lineal: El escalado lineal multiplica los datos por un factor constante para ajustar la amplitud de la señal.

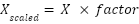
Código de Ejemplo Implementación en ESP32:

#define NUM_SAMPLES 100
#define SCALE_FACTOR 0.5

float data[NUM_SAMPLES];
float scaledData[NUM_SAMPLES];

void setup() {
  Serial.begin(115200);

  // Simular datos de entrada
  for (int i = 0; i < NUM_SAMPLES; i++) {
    data[i] = analogRead(34); // Leer el valor del ADC
  }

  // Escalar los datos
  for (int i = 0; i < NUM_SAMPLES; i++) {
    scaledData[i] = data[i] * SCALE_FACTOR;
  }

  // Imprimir los datos escalados
  for (int i = 0; i < NUM_SAMPLES; i++) {
    Serial.println(scaledData[i]);
  }
}

void loop() {
  // No se necesita código en el loop para este ejemplo
}

Escalado robusto: El escalado robusto (Robust Scaling) es una técnica que utiliza estadísticos robustos (mediana y rango intercuartílico) en lugar de la media y la desviación estándar. Esta técnica es menos sensible a los valores atípicos y más adecuada cuando los datos contienen muchos outliers ( punto de datos que se encuentra significativamente alejado de otros puntos de datos en un conjunto). Por otro lado puede ser más complicado de implementar y calcular y no garantiza que los valores estén en un rango específico (como [0, 1]).

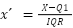
Donde

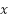es el valor original de la característica

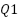es el primer cuartil (25%)

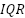Es el rango intercuartílico (diferencia entre el tercer cuartil y el primer cuartil, Q3−Q1)).

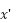es el valor escalado.

Código de Ejemplo Implementación en ESP32:

#include <Arduino.h>
#include <algorithm> // Necesario para std::sort

double median(double* data, int size) {
  std::sort(data, data + size);
  if (size % 2 == 0) {
    return (data[size / 2 - 1] + data[size / 2]) / 2.0;
  } else {
    return data[size / 2];
  }
}

void scaleRobust(double* data, int size) {
  double q1, q3, iqr;
  double sortedData[size];
  
  // Copiar los datos para ordenarlos
  memcpy(sortedData, data, size * sizeof(double));
  
  // Calcular el primer cuartil (Q1) y el tercer cuartil (Q3)
  q1 = median(sortedData, size / 2);
  q3 = median(sortedData + size / 2, size - size / 2);
  
  // Calcular el rango intercuartílico (IQR)
  iqr = q3 - q1;
  
  // Escalar los datos
  for (int i = 0; i < size; i++) {
    data[i] = (data[i] - q1) / iqr;
  }
}

void setup() {
  Serial.begin(115200);
  double data[] = {1.0, 2.0, 3.0, 4.0, 100.0}; // Nota: 100 es un outlier
  int size = sizeof(data) / sizeof(data[0]);

  scaleRobust(data, size);
  
  Serial.println("Datos escalados (Robusto):");
  for (int i = 0; i < size; i++) {
    Serial.println(data[i]);
  }
}

void loop() {
  // No se necesita código en el loop para este ejemplo
}

Aplicaciones en Sistemas Embebidos

La normalización y el escalado tienen varias aplicaciones en sistemas embebidos. Son útiles para el pre-procesamiento de datos de sensores dado que ajusta las lecturas de sensores para que sean consistentes y comparables. Además mejoran la precisión de algoritmos de machine learning embebidos. Otro aspecto importante es que estas técnicas ayudan a la visualización de datos usando interfaces gráficas o herramientas de monitoreo, reducen el ruido eliminando variaciones no deseadas en los datos para mejorar la detección de patrones y mejoran el rendimiento de los algoritmos asegurando que los datos están dentro de un rango específico para mejorar la convergencia y el rendimiento de algoritmos de control y aprendizaje automático.

La reducción de dimensionalidad es una técnica de procesamiento de datos que transforma datos de alta dimensionalidad a un espacio de menor dimensión sin perder información significativa. En Sistemas Embebidos, donde los recursos computacionales y de memoria son limitados, la reducción de dimensionalidad es crucial para mejorar la eficiencia y la capacidad de procesamiento.

Reducción de Dimensionalidad

La reducción de dimensionalidad implica transformar un conjunto de datos con muchas características (dimensiones) en un conjunto de datos con menos características. Los métodos más comunes son:

• Análisis de Componentes Principales (PCA): Un método lineal que transforma los datos a un nuevo espacio de menor dimensión utilizando combinaciones lineales de las características originales que capturan la mayor variabilidad en los datos.
• Análisis de Componentes Independientes (ICA): Similar a PCA pero enfocado en encontrar componentes estadísticamente independientes en lugar de componentes ortogonales.
• t-Distributed Stochastic Neighbor Embedding (t-SNE): Un método no lineal que es útil para la visualización en espacios de baja dimensionalidad, preservando las relaciones locales en los datos.
• Autoencoders: Redes neuronales que se entrenan para reconstruir la entrada en la salida, utilizando una capa oculta de menor dimensión que actúa como una representación comprimida.

Implementación en una ESP32

Para ilustrar la implementación de PCA en una ESP32, se utiliza un conjunto de datos simples, por ejemplo, lecturas de sensores de un acelerómetro en tres ejes (X, Y, Z). La idea es reducir estas tres dimensiones a dos dimensiones para simplificar el análisis y visualización.

Ejemplo de Implementación

1. Recolectar y Normalizar los Datos

Primero, se requiere recolectar las lecturas del sensor y normalizarlas.

#include <Wire.h>
#include <Adafruit_Sensor.h>
#include <Adafruit_MPU6050.h>

#define NUM_SAMPLES 100 // Número de muestras
#define DIMENSIONS 3 // Número de dimensiones originales (X, Y, Z)
#define REDUCED_DIMENSIONS 2 // Número de dimensiones reducidas

Adafruit_MPU6050 mpu;
float data[NUM_SAMPLES][DIMENSIONS]; // Matriz para almacenar las muestras
float mean[DIMENSIONS]; // Para almacenar las medias de cada dimensión

void setup() {
  Serial.begin(115200);
  if (!mpu.begin()) {
    Serial.println("Failed to find MPU6050 chip");
    while (1) {
      delay(10);
    }
  }
  mpu.setAccelerometerRange(MPU6050_RANGE_2_G);
  mpu.setGyroRange(MPU6050_RANGE_250_DEG);
  mpu.setFilterBandwidth(MPU6050_BAND_21_HZ);

  // Recolectar datos
  for (int i = 0; i < NUM_SAMPLES; i++) {
    sensors_event_t a, g, temp;
    mpu.getEvent(&a, &g, &temp);
    data[i][0] = a.acceleration.x;
    data[i][1] = a.acceleration.y;
    data[i][2] = a.acceleration.z;
    delay(10); // Esperar 10 ms entre lecturas
  }

  // Calcular medias
  for (int j = 0; j < DIMENSIONS; j++) {
    mean[j] = 0;
    for (int i = 0; i < NUM_SAMPLES; i++) {
      mean[j] += data[i][j];
    }
    mean[j] /= NUM_SAMPLES;
  }

  // Restar medias (centrar los datos)
  for (int j = 0; j < DIMENSIONS; j++) {
    for (int i = 0; i < NUM_SAMPLES; i++) {
      data[i][j] -= mean[j];
    }
  }

  // Imprimir datos normalizados
  Serial.println("Datos Normalizados:");
  for (int i = 0; i < NUM_SAMPLES; i++) {
    Serial.print(data[i][0]); Serial.print(", ");
    Serial.print(data[i][1]); Serial.print(", ");
    Serial.print(data[i][2]); Serial.println();
  }
}

2. Calcular la Matriz de Covarianza

float covarianceMatrix[DIMENSIONS][DIMENSIONS];

void calculateCovarianceMatrix() {
  for (int i = 0; i < DIMENSIONS; i++) {
    for (int j = 0; j < DIMENSIONS; j++) {
      covarianceMatrix[i][j] = 0;
      for (int k = 0; k < NUM_SAMPLES; k++) {
        covarianceMatrix[i][j] += data[k][i] * data[k][j];
      }
      covarianceMatrix[i][j] /= (NUM_SAMPLES - 1);
    }
  }
}

void printMatrix(float matrix[DIMENSIONS][DIMENSIONS]) {
  for (int i = 0; i < DIMENSIONS; i++) {
    for (int j = 0; j < DIMENSIONS; j++) {
      Serial.print(matrix[i][j]);
      Serial.print(" ");
    }
    Serial.println();
  }
}

void loop() {
  calculateCovarianceMatrix();
  Serial.println("Matriz de Covarianza:");
  printMatrix(covarianceMatrix);
  while (1) {
    // Para que el loop no haga nada después
  }
}

3. Calcular los Vectores y Valores Propios (Eigenvalues y Eigenvectors)

Debido a la complejidad de los cálculos de valores propios en un microcontrolador como la ESP32, se recomienda usar herramientas externas para calcular estos valores (por ejemplo, MATLAB, Python con NumPy) y luego usar esos resultados en el código embebido para proyectar los datos a un espacio reducido.

4. Proyección de Datos a Espacio Reducido

float eigenvectors[DIMENSIONS][REDUCED_DIMENSIONS] = {
  {0.577, -0.707}, // Ejemplo de vectores propios pre-calculados
  {0.577, 0.000},
  {0.577, 0.707}
};

float reducedData[NUM_SAMPLES][REDUCED_DIMENSIONS];

void projectData() {
  for (int i = 0; i < NUM_SAMPLES; i++) {
    for (int j = 0; j < REDUCED_DIMENSIONS; j++) {
      reducedData[i][j] = 0;
      for (int k = 0; k < DIMENSIONS; k++) {
        reducedData[i][j] += data[i][k] * eigenvectors[k][j];
      }
    }
  }
}

void loop() {
  projectData();
  Serial.println("Datos Reducidos:");
  for (int i = 0; i < NUM_SAMPLES; i++) {
    Serial.print(reducedData[i][0]); Serial.print(", ");
    Serial.println(reducedData[i][1]);
  }
  while (1) {
    // Para que el loop no haga nada después
  }
}

Aplicaciones en Sistemas Embebidos

La reducción de dimensionalidad tiene varias aplicaciones en sistemas embebidos:

• Compresión de Datos: Reducir el tamaño de los datos para almacenamiento y transmisión más eficiente.
• Visualización de Datos: Facilitar la visualización de datos en espacios de baja dimensionalidad.
• Preprocesamiento para Machine Learning: Mejorar la eficiencia y el rendimiento de algoritmos de aprendizaje automático al reducir la dimensionalidad de los datos de entrada.
• Eliminación de ruido: Al enfocarse en las principales componentes de variación, se pueden eliminar componentes ruidosas.

La reducción de dimensionalidad es una técnica poderosa para mejorar la eficiencia del procesamiento de datos en sistemas embebidos. Utilizando métodos como PCA, es posible simplificar el análisis de datos, reducir el ruido y mejorar el rendimiento de los algoritmos de machine learning, incluso en dispositivos con recursos limitados como la ESP32. La implementación adecuada de estas técnicas puede transformar la manera en que se manejan y analizan los datos en aplicaciones embebidas.