En esta sección, implementaremos una neurona en Verilog, abordando tanto la lógica para la operación de suma ponderada como la implementación de la función de activación. Verilog es ideal para este tipo de diseño debido a su capacidad para describir operaciones concurrentes y optimizar el hardware resultante para ejecutar estas operaciones de manera eficiente.

Implementación de la Neurona en Verilog.

La implementación de una neurona en Verilog se puede desglosar en dos módulos principales: el módulo que realiza la suma ponderada de las entradas y el módulo que aplica la función de activación. A continuación, se presentan ambos códigos.

Módulo de la Neurona: Suma Ponderada: Este módulo toma como entradas las señales inputs y weights, que representan las entradas a la neurona y sus pesos respectivos. Calcula la suma ponderada y la pasa a la siguiente etapa, que es la función de activación.

module Neuron (
    input [7:0] input1,  // Entrada 1 de 8 bits
    input [7:0] input2,  // Entrada 2 de 8 bits
    input [7:0] weight1, // Peso para la entrada 1
    input [7:0] weight2, // Peso para la entrada 2
    output [15:0] weighted_sum  // Salida de la suma ponderada
);
    wire [15:0] product1;
    wire [15:0] product2;

    // Multiplicaciones
    assign product1 = input1 * weight1;
    assign product2 = input2 * weight2;

    // Suma ponderada
    assign weighted_sum = product1 + product2;
endmodule

En este código, se realizan dos multiplicaciones en paralelo (input1 * weight1 y input2 * weight2), seguidas de una suma para obtener la salida ponderada. La salida weighted_sum es el resultado que se alimentará a la función de activación.

Módulo de la Función de Activación: ReLU: A continuación, implementamos una función de activación tipo ReLU (Rectified Linear Unit), que devuelve el valor de entrada si es positivo, y 0 si es negativo. La ReLU es ampliamente utilizada en redes neuronales debido a su simplicidad y eficacia.

module ReLU (
    input [15:0] weighted_sum,  // Entrada de la suma ponderada
    output [15:0] activated_output  // Salida después de la activación
);
    // Implementación de la función ReLU
    assign activated_output = (weighted_sum[15] == 1'b0) ? weighted_sum : 16'd0;
endmodule

En este módulo, el bit más significativo (weighted_sum[15]) indica el signo de la entrada (0 para positivo y 1 para negativo). La salida es la misma que la entrada si es positiva, o 0 si es negativa.

Integración de la Neurona Completa: Finalmente, integramos ambos módulos en un módulo completo que representa la neurona.

module CompleteNeuron (
    input [7:0] input1, 
    input [7:0] input2, 
    input [7:0] weight1, 
    input [7:0] weight2, 
    output [15:0] neuron_output
);
    wire [15:0] weighted_sum;

    // Instancia del módulo de suma ponderada
    Neuron neuron_instance (
        .input1(input1),
        .input2(input2),
        .weight1(weight1),
        .weight2(weight2),
        .weighted_sum(weighted_sum)
    );

    // Instancia del módulo ReLU
    ReLU relu_instance (
        .weighted_sum(weighted_sum),
        .activated_output(neuron_output)
    );
endmodule

En este módulo CompleteNeuron, las entradas input1, input2, weight1, y weight2 son procesadas para generar una salida neuron_output que es el resultado de la suma ponderada seguida por la función de activación ReLU.

Ejecución en un Microcontrolador de un Solo Núcleo

En un microcontrolador de un solo núcleo, la ejecución de la misma operación requiere procesar las instrucciones secuencialmente. Un pseudocódigo para la implementación en un microcontrolador podría ser el siguiente:

int input1 = ...;
int input2 = ...;
int weight1 = ...;
int weight2 = ...;
int product1, product2, weighted_sum, neuron_output;

// Multiplicación de las entradas por sus pesos
product1 = input1 * weight1;
product2 = input2 * weight2;

// Suma ponderada
weighted_sum = product1 + product2;

// Aplicación de la función ReLU
if (weighted_sum > 0) {
    neuron_output = weighted_sum;
} else {
    neuron_output = 0;
}

Este código se ejecuta secuencialmente, lo que significa que el microcontrolador procesa una instrucción a la vez: primero realiza las multiplicaciones, luego suma los resultados y, finalmente, aplica la función de activación. Esta secuencia implica que, para un cálculo como este, el tiempo total de ejecución es la suma de los tiempos de ejecución individuales de cada operación.

Ejecución en FPGA con Verilog.

Por otro lado, en una FPGA, gracias a su capacidad para la ejecución concurrente, las operaciones de multiplicación y suma pueden realizarse simultáneamente en diferentes bloques lógicos. En la implementación en Verilog presentada anteriormente:

Las dos multiplicaciones (input1 * weight1 y input2 * weight2) se realizan en paralelo. La suma de los productos ocurre inmediatamente después de que los productos estén disponibles. La función de activación también se aplica de inmediato, utilizando una sencilla comparación de un solo ciclo de reloj.

Esto significa que, en términos de latencia, la FPGA ejecuta todas estas operaciones en menos ciclos de reloj en comparación con un microcontrolador, donde las operaciones deben ejecutarse secuencialmente. En un diseño bien optimizado en FPGA, estas operaciones pueden completarse en un solo ciclo de reloj, dado que el hardware está configurado para operar en paralelo.

Consideraciones de Rendimiento.

• Latencia: La implementación en FPGA tiene una latencia mucho menor debido a la ejecución concurrente. En contraste, el microcontrolador tiene una latencia acumulativa debido a la ejecución secuencial.
• Consumo de Energía: Aunque depende del diseño específico, las FPGAs generalmente son más eficientes energéticamente para tareas específicas como esta, ya que cada operación está optimizada para el hardware. Un microcontrolador ejecutando en un ciclo de reloj más alto para completar la misma tarea podría consumir más energía.
• Flexibilidad vs. Eficiencia: Los microcontroladores son más flexibles en cuanto a programación y pueden realizar una variedad de tareas, mientras que la FPGA está optimizada para esta tarea en particular. Sin embargo, una vez que la FPGA está configurada, es mucho más rápida y eficiente para esa tarea específica.

En conclusión, la implementación de una neurona en una FPGA utilizando Verilog ofrece una solución mucho más rápida y eficiente en comparación con un microcontrolador convencional de un solo núcleo. Esto es particularmente relevante en aplicaciones de IA embebida donde la velocidad y la eficiencia energética son críticas.

Sigmoide.

La función de activación sigmoide, que es otra de las funciones de activación comúnmente utilizadas en redes neuronales se define como:

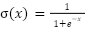
Sin embargo, implementar la función sigmoide en hardware puede ser costoso en términos de recursos debido a la operación de exponenciación y la división. Por lo tanto, es común utilizar una aproximación a la función sigmoide para facilitar su implementación en hardware. Una aproximación lineal por partes es una opción sencilla. La idea es dividir el rango de entrada en segmentos y aproximar la sigmoide con segmentos lineales.

module Sigmoid (
    input signed [15:0] weighted_sum,  // Entrada de la suma ponderada
    output reg [15:0] activated_output  // Salida después de la activación
);
    always @(*) begin
        if (weighted_sum < -16'd1024) begin
            activated_output = 16'd0;  // Aproximación a 0
        end else if (weighted_sum > 16'd1024) begin
            activated_output = 16'd65535;  // Aproximación a 1 (valor máximo de 16 bits)
        end else begin
            // Aproximación lineal entre -1024 y 1024
            activated_output = (weighted_sum + 16'd1024) * 16'd32;
        end
    end
endmodule

En este módulo, la función sigmoide se aproxima de la siguiente manera:

Saturación: Para valores de entrada muy negativos (weighted_sum < -1024), la salida se aproxima a 0. Para valores de entrada muy positivos (weighted_sum > 1024), la salida se aproxima a 1 (representado por 65535 en formato de 16 bits).

Aproximación Lineal: Entre los valores -1024 y 1024, la función sigmoide se aproxima linealmente. La salida es escalada para cubrir todo el rango de 16 bits. Esta es una simplificación considerable que hace que la implementación sea mucho más eficiente en términos de recursos hardware, sacrificando un poco de precisión a cambio de simplicidad y velocidad.

Integración en la Neurona Completa: Ahora se puede integrar esta función de activación sigmoide en la neurona completa, sustituyendo la función ReLU implementada previamente.

module CompleteNeuronSigmoid (
    input [7:0] input1, 
    input [7:0] input2, 
    input [7:0] weight1, 
    input [7:0] weight2, 
    output [15:0] neuron_output
);
    wire [15:0] weighted_sum;

    // Instancia del módulo de suma ponderada
    Neuron neuron_instance (
        .input1(input1),
        .input2(input2),
        .weight1(weight1),
        .weight2(weight2),
        .weighted_sum(weighted_sum)
    );

    // Instancia del módulo Sigmoid
    Sigmoid sigmoid_instance (
        .weighted_sum(weighted_sum),
        .activated_output(neuron_output)
    );
endmodule

Tanh (Tangente Hiperbólica)

La función de activación Tanh (Tangente Hiperbólica) es otra función de activación comúnmente utilizada en redes neuronales y está definida como:

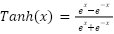
La función Tanh mapea los valores de entrada a un rango entre -1 y 1, lo que puede ser útil para modelos donde se espera que las salidas sean tanto negativas como positivas.

Al igual que con la sigmoide, implementar Tanh en hardware de manera exacta es costoso en términos de recursos debido a la necesidad de operaciones exponenciales. Por lo tanto, también utilizaremos una aproximación para facilitar su implementación en hardware.

A continuación, se presenta una implementación aproximada de la función Tanh utilizando Verilog. Esta aproximación se basa en dividir el rango de entrada en segmentos y aproximar Tanh con funciones lineales por partes.

module Tanh (
    input signed [15:0] weighted_sum,  // Entrada de la suma ponderada
    output reg signed [15:0] activated_output  // Salida después de la activación
);
    always @(*) begin
        if (weighted_sum < -16'd1024) begin
            activated_output = -16'd32768;  // Aproximación a -1 (valor mínimo de 16 bits)
        end else if (weighted_sum > 16'd1024) begin
            activated_output = 16'd32767;  // Aproximación a 1 (valor máximo de 16 bits)
        end else begin
            // Aproximación lineal entre -1024 y 1024
            activated_output = weighted_sum * 16'd32;  // Escalado lineal
        end
    end
endmodule

En este módulo, la función Tanh se aproxima de la siguiente manera:

Saturación: Para valores de entrada muy negativos (weighted_sum < -1024), la salida se aproxima a -1, que se representa como -32768 en formato de 16 bits. Para valores de entrada muy positivos (weighted_sum > 1024), la salida se aproxima a 1, representado como 32767 en formato de 16 bits.

Aproximación Lineal: En el rango intermedio de -1024 a 1024, la función Tanh se aproxima con una función lineal. El valor de entrada se multiplica por un factor de 32 para escalar la salida a un rango apropiado dentro de los límites de 16 bits.

Comparación con la Función ReLU

En cuanto a complejidad de Implementación la función ReLU es extremadamente simple de implementar en hardware, requiriendo solo una comparación y una asignación condicional. Esto la hace muy eficiente en términos de recursos y latencia. La función sigmoide, incluso en su forma aproximada, es más compleja debido a la necesidad de manejar la saturación y la aproximación lineal. Requiere más operaciones lógicas y aritméticas, lo que puede aumentar el uso de LUTs y registros en la FPGA. La función Tanh, similar a la sigmoide, es más compleja de implementar en hardware debido a su forma no lineal. Sin embargo, con una aproximación adecuada, se puede implementar con un uso moderado de recursos.

Si hablamos de recursos y latencia, la función ReLU tiene una latencia mínima y utiliza muy pocos recursos de la FPGA. Por otro lado, la Sigmoide; aunque la versión aproximada presentada reduce significativamente la complejidad en comparación con la función sigmoide exacta, aún consume más recursos y tiene una latencia ligeramente mayor que ReLU. La Tanh tiene una complejidad similar a la sigmoide, con la ventaja de mapear la salida en un rango centrado en 0 (-1 a 1), lo que puede ser beneficioso en ciertas aplicaciones de redes neuronales.

La función ReLU es ideal para redes neuronales profundas donde la eficiencia y la simplicidad son prioritarias. Se utiliza principalmente en tareas de clasificación, reconocimiento de imágenes y procesamiento de señales. La Sigmoide es útil en aplicaciones donde la salida necesita estar en un rango específico (como entre 0 y 1), y en algunos modelos de redes neuronales más antiguas o en aplicaciones específicas como modelos probabilísticos. Tanh se utiliza a menudo en capas ocultas de redes neuronales, especialmente en situaciones donde las salidas negativas son significativas, como en tareas de regresión y procesamiento de señales.

La implementación de diferentes funciones de activación en hardware utilizando Verilog permite ajustar las características de una red neuronal a las necesidades específicas de la aplicación. Mientras que ReLU es preferible en términos de simplicidad y eficiencia, la función sigmoide, aunque más compleja, puede ser adecuada para aplicaciones donde se necesita una salida suavizada en un rango limitado. La selección de la función de activación y su implementación debe equilibrar la precisión requerida y los recursos disponibles en la FPGA.

La función de activación Tanh, implementada en Verilog, ofrece una opción más adecuada para tareas donde es importante que las salidas de la neurona tengan tanto valores positivos como negativos, y donde es necesario un mapeo más suave en un rango centrado en cero. Aunque es más compleja que ReLU en términos de implementación, la función Tanh, al igual que Sigmoide, es adecuada para aplicaciones específicas que requieren una salida más matizada, especialmente cuando se trata de modelos que deben lidiar con datos que pueden tener tanto entradas positivas como negativas. La implementación en hardware de estas funciones requiere un equilibrio entre la precisión, la eficiencia de los recursos y las necesidades específicas del modelo y la aplicación.