El ejemplo básico de la utilidad de los métodos de Monte Carlo es el del cálculo π por medio de aproximación. El objetivo de este ejemplo, es poder calcular el valor de π progresivamente, por medio de observaciones del ambiente.

En este caso, nuestro ambiente será un cuadrado de lado 2 en el plano cartesiano con un círculo de radio 1 y centro (0,0) definido dentro del cuadrado, como se muestra a continuación

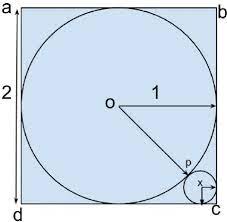
Figura 1. Círculo unitario en el plano cartesiano

Para el ambiente dado, los eventos de observación de nuestro algoritmo están definidos por la creación aleatoria de un punto en el plano. La recompensa de estos eventos está definida como 1, si el punto se encuentra dentro del círculo y 0 si el punto no se encuentra dentro del círculo, como se muestra a continuación.

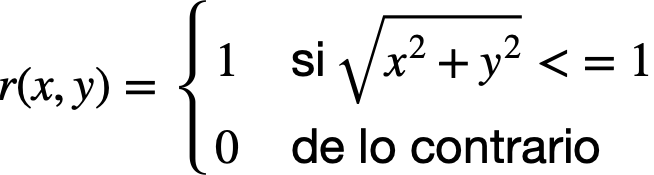
Para realizar el cálculo, el agente debe llevar una cuenta de los puntos que se han ubicado dentro del círculo y los que no, tomando la proporción entre estos dos conjuntos de puntos como una estimación de π.

El primer paso para aplicar el método de Monte Carlo consiste en la generación del punto a ubicar en el ambiente por medio de la función generate_points(size). En el contexto de los MDPs, este paso es equivalente a la escogencia aleatoria de la acción del agente.

montecarlo-pi.ipynb

def generate_points(size):
    x = random.random()*size
    y = random.random()*size
    return (x, y)        

Dado el punto generado, ahora es necesario observar si el punto se encuentra o no en el círculo, utilizando la fórmula de recompensa descrita anteriormente.

def is_in_circle(point, size):
    return math.sqrt(point[0]**2 + point[1]**2) <= size      

Finalmente, teniendo una cantidad de puntos generados hasta el momento, es posible aproximar el valor de π utilizando la fórmula del área del círculo.

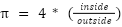
La razón para multiplicar la proporción de los puntos por 4 es que la evaluación se realiza únicamente en el cuadrante positivo del círculo.

Para demostrar el comportamiento del agente implementamos dos funciones de prueba, una para ver el cálculo progresivo del valor de π y otra que nos permita ver las observaciones del método de Monte Carlo.

Cálculo progresivo

Nuestra primera función de prueba calcula el valor de π dentro de cada iteración (i.e., episodio). Cada iteración del método de Monte Carlo consiste en tres pasos: (1) la generación de la observación (i.e., el punto), (2) el chequeo del resultado de la observación, y (3) el cálculo del valor del objetivo de la función. Este proceso se muestra a continuación.

def progressive_pi(sample_size):
    points_inside_circle = 0
    points_inside_square = 0
    for _ in range(sample_size):
        point = generate_points(square_size)
        if is_in_circle(point, square_size):
            points_inside_circle +=1
        points_inside_square += 1
        print("The value of pi so far is {}" .format(compute_pi(points_inside_circle, points_inside_square)))        

La ejecución de la función de prueba con distintos parámetros de iteración, deja ver como el método de Monte Carlo se acerca a el resultado correcto a medida que se van realizando más observaciones sobre el ambiente.

Este hecho es precisamente la razón por la cual el método de Monte Carlo es utilizado para la solución de los problemas de MDP.

Aproximación de π

La segunda función de prueba que utilizamos, muestra el cálculo completo de la aproximación de π, mostrando las observaciones generadas para 1000 observaciones

def full_pi(sample_size):
    points_inside_circle = 0
    points_inside_square = 0
    plt.axes().set_aspect('equal')
    plt.plot(1*np.cos(arc), 1*np.sin(arc))

    for _ in range(sample_size):
        point = generate_points(square_size)
        plt.plot(point[0], point[1], 'c.')
        points_inside_square += 1
        if is_in_circle(point, square_size):
            points_inside_circle += 1

    print("Approximate value of pi is {}" .format(compute_pi(points_inside_circle, points_inside_square)))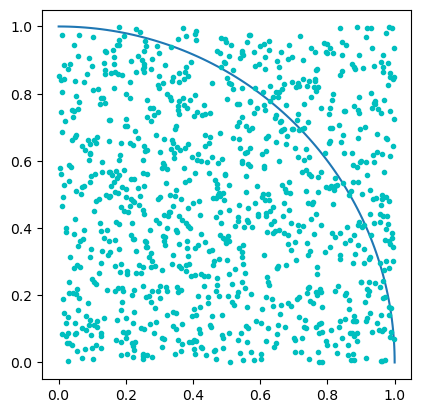

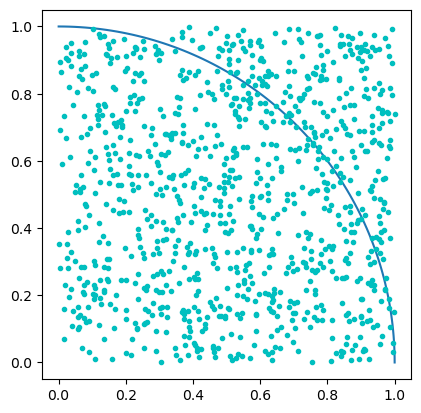
Figura 2. Valor calculado de π=3.19 Figura 3. Valor calculado de π=3.06

Intente ahora de poner toda la definición del cálculo de Monte Carlo junto y modifique la cantidad de iteraciones a ejecutar. ¿En qué punto la aproximación es precisa?

Licencia

© - Derechos Reservados: La presente obra, y en general todos sus contenidos, se encuentran protegidos por las normas internacionales y nacionales vigentes sobre propiedad Intelectual, por lo tanto su utilización parcial o total, reproducción, comunicación pública, transformación, distribución, alquiler, préstamo público e importación, total o parcial, en todo o en parte, en formato impreso o digital y en cualquier formato conocido o por conocer, se encuentran prohibidos, y solo serán lícitos en la medida en que se cuente con la autorización previa y expresa por escrito de la Universidad de los Andes.

De igual manera, la utilización de la imagen de las personas, docentes o estudiantes, sin su previa autorización está expresamente prohibida. En caso de incumplirse con lo mencionado, se procederá de conformidad con los reglamentos y políticas de la universidad, sin perjuicio de las demás acciones legales aplicables.

Creadores

Nicolás Cardozo, Profesor Asociado

Camilo Cabrera, Tutor

Facultad de Ingeniería

Departamento de Ingeniería de Sistemas y Computación

Universidad de los Andes

Bogotá, Colombia

Enero, 2023