Ambiente de Bandidos

En este tutorial construiremos un ambiente de pruebas para los diferentes escenarios del problema de los bandidos de k-brazos. Para ello debemos definir:

Un bandido, donde sea posible parametrizar las posibilidades a escoger.
La distribución de las recompensas para cada una de las máquinas.
Medir la efectividad del bandido por medio de la ejecución de múltiples escenarios.

Durante este tutorial debe implementar el bandido y el ambiente de prueba en Jupyter notebooks (o desde su máquina local) a medida que se van dando las explicaciones.

(1)Inicialmente crearemos un bandido de k-brazos con un comportamiento constante. (2) Probaremos su comportamiento por medio de una gráfica. (3) Luego le daremos aleatoriedad a las recompensas de escoger cada uno de los brazos y veremos el comportamiento acumulado de cada uno de los brazos, como de la recompensa esperada total del bandido.

La definición de los bandidos consiste en crear un agente, como una clase de Python, Bandit (bandit.py). Inicialmente crearemos un bandido con una cantidad de brazos dado por parámetro (por defecto utilizaremos 10 brazos).

Cada uno de los brazos del bandido (definidos en una lista como un atributo de la clase) tiene su propia recompensa, la cual asignaremos como un número flotante aleatorio en el rango [-3,3] (utilizando la función random.uniform(-3,3) de la librería random). Adicionalmente, definimos un atributo de la clase (reward) para mantener la recompensa cumulativa del bandido.

Inicialmente nuestro bandido tiene dos funciones choose_arm y run.

expected_reward no tienen parámetros (excepto el parámetro self por defecto de las clases de Python). Esta función se encarga de seleccionar un brazo a ejecutar, de forma aleatoria, y retorna la recompensa recibida de acuerdo a la fórmula:

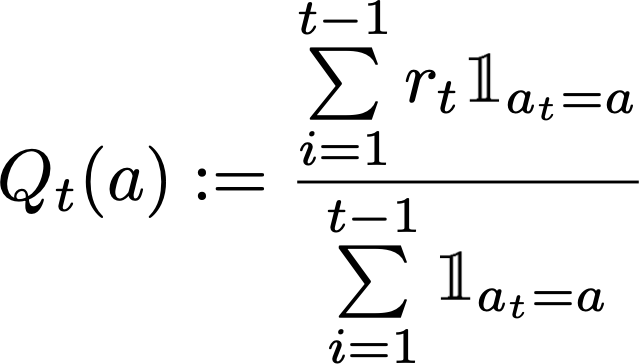
Retornando la recompensa promedio obtenida por el agente al escoger el brazo dado.

Para poder realizar este cálculo, debemos llevar la cuenta de la cantidad de veces que ha sido escogido cada brazo y la recompensa acumulada de cada brazo. Esta información la definimos como atributos de la clase, en las variables occurrences y cumulative_rewards, respectivamente. Ambos atributos se definen como una lista de tamaño número de brazos del bandido.

El cálculo de la recompensa primero actualiza las ocurrencias de escoger el brazo seleccionado aleatoriamente, arm. Además debemos actualizar la recompensa cumulativa de arm, sumando la recompensa correspondiente al brazo (obtenida de la lista de brazos). Finalmente, calculamos Q_t(a) como la recompensa cumulativa sobre las ocurrencias para el brazo dado y retornamos dicho valor. La recompensa global del agente se actualiza con el valor calculado.

run no recibe ningún parámetro. Esta función define la cantidad de episodios para los cuales vamos a calcular la recompensa del agente (1000 en nuestro caso)

Luego creamos un bandido (bandit) y una variable para almacenar la recompensa obtenida en cada iteración (expected_reward).

Para cada uno de los episodios, ejecutamos el bandido llamando la función choose_arm y guardamos el resultado en la lista de recompensas esperadas.

Finalmente retornamos la lista de recompensas para cada iteración (expected_reward).

Ejemplo

Suponga que tenemos un bandido de 4 brazos con recompensas 10, 3, 15 y 7 como se muestra a continuación.

El bandido tiene un valor esperado para la recompensa de cada brazo Q_t(a) como se muestra en la tabla a continuación.

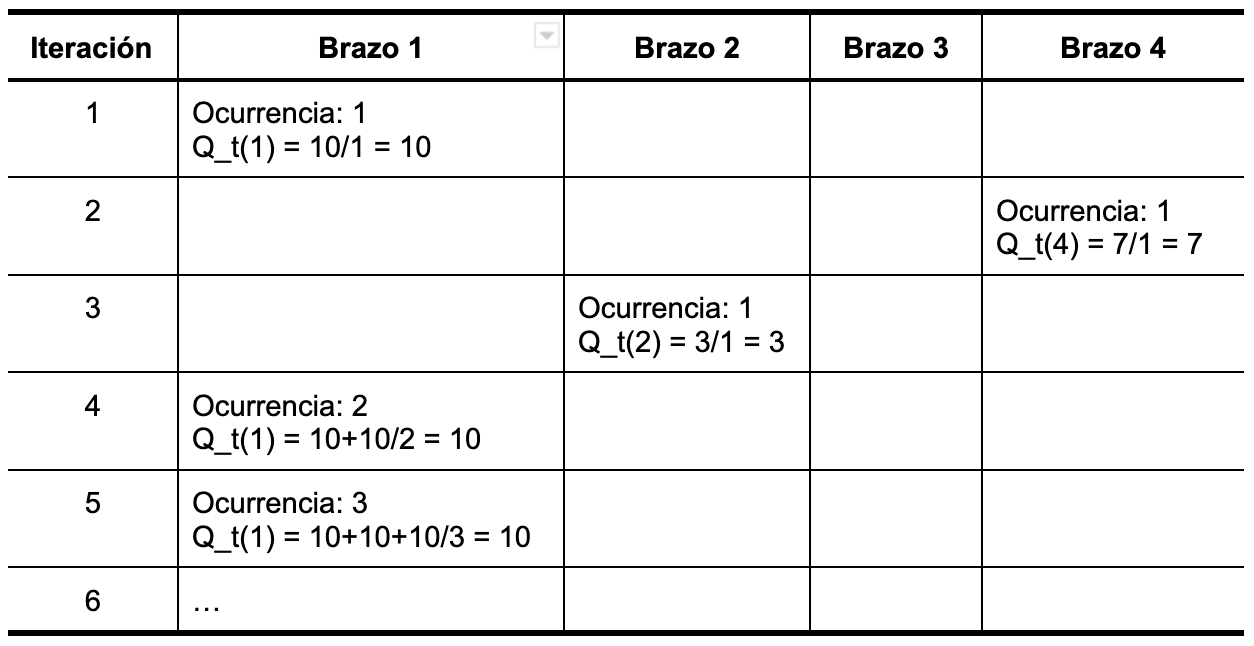
Como es posible ver, a medida que seleccionamos los brazos, vamos obteniendo un valor de recompensa esperada. Para esta versión inicial del agente, la recompensa es constante, para cada uno de los brazos.

Nuestro ambiente de evaluación consiste en ejecutar uno o múltiples bandidos. Para ello utilizaremos la librería matplotlib (https://matplotlib.org/) para crear un script que nos permita observar el rendimiento del bandido con respecto a la recompensa obtenida.

El siguiente fragmento de código muestra la definición de una gráfica sencilla, definiendo la cantidad de iteraciones a evaluar (1,000 en nuestro caso) y los labels de la gráfica. En este fragmento, la Línea 4 define la variable dependiente a graficar, la cual será el número de iteraciones/ejecuciones del bandido. La línea 5 define el ambiente de la gráfica y las líneas 6 a 8 definen los nombres de la gráfica y sus ejes.

graph.py

import matplotlib.pyplot as plt
import numpy as np
from bandit import *

# get data
x = np.linspace(0, 1000, 1000)

# plot
fig, ax = plt.subplots()
plt.title("Bandit average reward")
plt.xlabel("Iterations")
plt.ylabel("Average reward")

Para obtener los datos a graficar, definimos una función llamada plot_bandits, que recibe como parámetro el número de bandidos que vamos a evaluar.

Dentro de la función debemos crear tantos bandidos como sean pasados por parámetro y ejecutarlos.

Para ejecutar un bandido debemos llamar la función run definida anteriormente.
El resultado de dicha función se debe convertir a un arreglo de numpy para poder graficarlo como la variable dependiente (y) de la gráfica. Esto se puede realizar directamente creando un arreglo np.array con parámetro el llamado a la función run.
Finalmente, debemos agregar los datos x y y a la gráfica por medio de la función ax.plot(x, y, linewidth=2.0, label=f'bandit {i}')

Una vez definidos los bandidos, debemos agregar la leyenda a la gráfica y mostrar los datos, respectivamente llamando las funciones ax.legend() y plt.show().

Para ejecutar el ambiente de los bandidos, simplemente debemos llamar la función plot_bandits con el número de bandidos que queremos ejecutar.

Ejercicio

Ejecute plot_bandits múltiples veces con 1, 2, 3 y 4 bandidos.

¿Nota alguna diferencia entre las ejecuciones?

¿A qué se debe la diferencia (si la hay)?

Teniendo en cuenta que las máquinas de azar no dan una recompensa cada vez que son escogidas, como en la vida real, nuestro bandido tampoco debería tener una recompensa constante. Para ello modificaremos la recompensa de cada brazo para que retorne el valor completo de la recompensa con una probabilidad del 50% y que otorgue una fracción de la recompensa (r/# de brazo + 1) con una probabilidad del 50%. Es decir la recompensa será r/2 para el brazo 1, r/3 para el brazo 2 y así sucesivamente.

Para hacer esto debemos modificar la función choose_arm, cambiando la forma en que actualizamos la recompensa cumulativa de cada brazo. Antes de actualizar el valor debemos saber cual es el valor a actualizar. Esta división la hacemos por medio de un condicional sobre una nueva variable aleatoria. Si el valor es menor que 0.5, retornará la recompensa completa, de lo contrario retornará la fracción de la recompensa correspondiente.

Ejemplo

Suponga que tenemos un bandido de 4 brazos con recompensas 10, 3, 15 y 7 como se muestra a continuación.

El bandido tiene un valor esperado para la recompensa de cada brazo Q_t(a) como se muestra en la tabla a continuación. Para efectos de este ejemplo, las iteraciones pares son aquellas que retornarán una fracción de la recompensa.

Finalmente modificaremos el bandido para recibir un parámetro que indique si queremos graficar la recompensa total del bandido ("t"), o la recompensa cumulativa de cada brazo ("c") (como veníamos haciendo). Este parámetro se debe agregar a la función run y choose_arm de Bandit. En esta última función debemos decidir qué valor retornar de acuerdo a dicho parámetro. Igualmente debemos agregar el parámetro a la función plot_bandits de nuestro script graph.py.

Ejercicio

Ejecute plot_bandits con diferentes parámetros "t" y "c".

¿Nota alguna diferencia entre las ejecuciones?

¿Que se puede decir sobre el comportamiento de la recompensa total cuando se ejecuta con el parámetro "t"?

© - Derechos Reservados: La presente obra, y en general todos sus contenidos, se encuentran protegidos por las normas internacionales y nacionales vigentes sobre propiedad Intelectual, por lo tanto su utilización parcial o total, reproducción, comunicación pública, transformación, distribución, alquiler, préstamo público e importación, total o parcial, en todo o en parte, en formato impreso o digital y en cualquier formato conocido o por conocer, se encuentran prohibidos, y solo serán lícitos en la medida en que se cuente con la autorización previa y expresa por escrito de la Universidad de los Andes.

De igual manera, la utilización de la imagen de las personas, docentes o estudiantes, sin su previa autorización está expresamente prohibida. En caso de incumplirse con lo mencionado, se procederá de conformidad con los reglamentos y políticas de la universidad, sin perjuicio de las demás acciones legales aplicables.

Recursos Digitales

Nicolás Cardozo, Profesor Asociado

Facultad de Ingeniería

Departamento de Ingeniería de Sistemas y Computación

Universidad de los Andes

Bogotá, Colombia

Enero, 2023